4.4. Решение задачи линейного программирования в рамках построенной модели

1. Графический метод решения.

Рассмотрим задачу линейного программирования с двумя переменным

при наличии ограничений:

Каждое неравенство системы ограничений задачи геометрически определяет полуплоскость с границей (граничные прямые). Условие неотрицательности определяет точки первой координатной четверти. Если система неравенств совместна, то область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Совокупность этих точек будем называть многоугольником решений или областью допустимых решений задачи линейного программирования. Стороны этого многоугольника образованы прямыми (граничные прямые).

Областью допустимых решений системы неравенств могут быть:

выпуклый многоугольник, выпуклая многоугольная неограниченная область, пустая область, луч, отрезок, единственная точка.

Целевая функция L определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение L. Целевая функция, заданная уравнением , проходит через начало координат и называется основной прямой. Вектор перпендикулярный этой прямой, указывает направление максимального роста функции L, а противоположный вектор – направление максимального убывания L.

Геометрическая интерпретация задачи линейного программирования заключается в нахождении (построении) многоугольника решений, каждая точка которого является допустимым решением. Среди этого множества решений необходимо отыскать такую точку, координаты которой обращают в min или max целевую функцию. Если задача линейного программирования имеет оптимальный план, то целевая функция задачи принимает свое оптимальное значение в одной из вершин многоугольника решений.

Для определения данной вершины строится прямая L = 0, проходящая через начало координат и перпендикулярно вектору , и перемешается в направлении этого вектора до тех пор, пока она не коснется последней крайней точки многоугольника решений. Координаты полученной точки определяют оптимальный (максимальный) план данной задачи, а значение функции максимальное значение целевой функции L.

Нахождение минимального значения L отличается от нахождения ее максимального значения лишь тем, что L = 0 передвигается не в направлении вектора , а в противоположном направлении.

Если в направлении вектора многоугольник решений неограничен, то целевая функция неограничена (не имеет максимального значения).

Итак, графический метод решения включает следующие этапы:

– строят граничные прямые, уравнения которых получают в результате замены в системе ограничений знаков неравенств на знак равенства;

– находят полуплоскости, определяемые каждым из ограничений неравенств;

– находят многоугольник решений (область допустимых решений);

– строят основную прямую , проходящую через начало координат и перпендикулярную вектору целевой функции ;

– перемещают прямую L = 0 в направлении вектора или в противоположном направлении вектора . В результате находят точку (точки), в которой целевая функция принимает оптимальное решение, либо устанавливают неограниченность функции на множестве планов.

Пример. Для производства двух видов изделий А и В можно использовать сырьё трёх видов. При этом на изготовление единицы изделия А расходуется 4 ед. сырья первого вида, 2 – ед. 2-го и 3 – 3-го вида. На изготовление единицы изделия В расходуется 2 ед. сырья 1-го вида, 5 ед. 2-го вида, 4 ед. 3-го вида сырья. На складе фабрики имеется 35 ед. сырья 1-го вида, 43 ед. 2-го вида и 40 ед. 3 – го вида. От реализации единицы готовой продукции вида А фабрика имеет прибыль 5 тыс. руб., а от продукции вида В прибыль составляет 9 тыс. руб.

Составить математическую модель исходной задачи. Найти решение графически методом.

По данным задачи составим таблицу:

Вид сырья	Запасы сырья	Расход сырья на 1 ед. продукции
		А	В
1 2 3	35 43 40	4 2 3	2 5 4
Прибыль от реализации 1 ед. продукции		5	9

Обозначим через х₁ и х₂ объемы выпускаемой продукции А и В соответственно. Затраты сырья первого вида составят , и они не должны превосходить запасов, т.е. 35 кг:

.

Аналогично: , .

Прибыль от реализации х₁ единиц изделия А и х₂ единиц изделия В составит – целевая функция задачи.

Получили модель задачи:

Вектор целевой функции имеет координаты: (5; 9).

По системе ограничений построим область на плоскости.

Для этого от неравенств перейдем к уравнениям и построим линии:

(1)

(2)

(3)

С помощью контрольной точки выбираем полуплоскость, координаты точек которой удовлетворяют неравенствам системы ограничений.

Для нахождения максимума целевой функции проведем из начала координат вектор целевой функции и перпендикулярную ему основную прямую (прямую ). Передвигаем основную прямую в направлении вектора целевой функции. В последней пересекаемой вершине многоугольника решений (точка А) получаем наибольшее значение целевой функции.

Найдем координаты точки А из системы:

.

оптимальный план.

Значение целевой функции в точке А: .

2. Симплекс-метод решения задачи линейного программирования.

Рассмотрим математическую модель стандартной задачи линейного программирования (система ограничений содержит знаки неравенств).

(7)

Предположим, что все свободные члены b_i системы неотрицательны. Приведём систему к основной (канонической), добавив в левые части неотрицательные свободные переменные х_n+1, …,х_n+m.

(8)

Системе (8) соответствует опорное решение

, в котором все основные неизвестные равны нулю, а базисные равны соответствующим свободным членам .

Симплексный метод – это метод последовательного улучшения опорного решения. Задача решается в симплексных таблицах.

		0	С1	С2		Сn	0	0		0
Ci	Баз	bi	x1	x2	…	xn	xn+1	xn+2	…	xn+m	Ө
0	xn+1	b1	a11	a12	…	a1n	1	0	…	0
0	xn+2	b2	a21	a22	…	a2n	0	1	…	0
-	-	-	-	-	-	-	-	-	-	-
0	xn+m	bm	am1	am2	…	amn	0	0	…	1
	Z	0	-C1	-C2		-Cn	0	0		0

Этой таблице соответствует опорное решение

Х₀=(0, 0, …,0, b₁, b₂, …, b_m) и соответствующее ему значение целевой функции Z₀=0.

Последняя строка таблицы называется оценочной и заполняется по формуле оценок: (9)

(Оценка при неизвестной x_к равна сумме произведений элементов первого столбца на соответствующие элементы столбца x_k минус с_k, стоящее над столбцом).

Условием оптимальности решения при Z→max является неотрицательность оценок ( ). Симплексным методом решается каноническая задача линейного программирования, у которой система ограничений каноническая, а целевая функция Z выражена через свободные неизвестные.

Алгоритм симплексного метода

1. Приводим систему ограничений задачи к канонической и записываем в симплексную таблицу Элементы оценочной строки вычисляются по формуле оценок (9).

2. Если среди оценок симплексной таблицы при решении на максимум нет отрицательных оценок, то соответствующее опорное решение является оптимальным.

3. Если в оценочной строке содержится отрицательная оценка, а в столбце над ней нет положительных элементов, то целевая функция не ограничена сверху на множестве допустимых (неотрицательных) решений. Задача не имеет оптимального решения.

4. Если в каждом столбце с отрицательной оценкой имеется хотя бы один положительный элемент, то переходим к ''лучшему'' опорному решению. Для этого:

а) выбираем разрешающий столбец по наименьшей отрицательной оценке;

б) выбираем разрешающую строку. Для этого вычисляем Ө как отношение свободных членов к положительным элементам разрешающего столбца. Выделяем разрешающий элемент, соответствующий наименьшему Ө;

в) элементы разрешающей строки делим на разрешающий элемент, записываем единичные столбцы, соответствующие базисным неизвестным;

г) элементы остальных строк вычисляем по формуле прямоугольников:

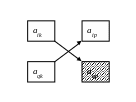
(10)

д) элементы оценочной строки также вычисляются по формуле «прямоугольников» и для контроля вычислений по формуле оценок.

Процесс вычислений продолжается до тех пор, пока не возникнут ситуации пунктов 1 или 2.

Решим пример, используя алгоритм.

Пример. На предприятии имеется три вида сырья и можно производить два вида продукции. Данные о расходе сырья на производство единицы продукции, запасов сырья и прибыли от реализации единицы продукции предоставлены в таблице:

Вид сырья	Запасы сырья	Расход сырья на 1 ед. продукции
		А	В
1 2 3	45 31 30	3 5 2	4 2 3
Прибыль от реализации 1 ед. продукции		7	5

Найти оптимальный план выпуска продукции, при котором предприятие получит наибольшую прибыль.

Решить задачу симплексным методом и графически.

Составим математическую модель. Обозначим через х₁ и х₂ выпуск продукции А и В соответственно. Затраты материала первого сорта на план (х₁, х₂) составят

3х₁ + 4х₂, и они не должны превосходить запасов, т.е. 45 кг:

3х₁ + 4х₂ 45.

Аналогичны ограничения по материалу второго сорта:

5х₁ + 2х₂ 35,

и по материалу третьего сорта

2х₁ + 3х₂ 30.

Прибыль от реализации х₁ единиц А и х₂ – В составит z = 7x₁ + 5x₂ – целевая функция задачи.

Получили модель задачи:

z = 7x₁ + 5x₂

Вводом переменных х₃, х₄, х₅ приводим модель к каноническому виду:

z = 7x₁ + 5x₂

Составим симплексную таблицу:

cj	базис (xj)	аi0	7	5	0	0	0
			х1	х2	х3	х4	х5
0 0 0	x3 x4 x5	45 31 30	3 5 2	4 2 3	1 0 0	0 1 0	0 0 1
	z	0	-7	-5	0	0	0

Первые три строки этой таблицы содержат в условной форме систему уравнений (ограничений) в канонической задаче, а именно: в столбцах a_i0 записываются в свободные члены уравнений, в столбцах х₁, х₂,..., х₅ – коэффициенты при соответствующих неизвестных этой системы.

Слева от столбца a_i0 в столбце x_j выписываются базисные неизвестные, содержащиеся в соответствующих уравнениях системы.

Верхняя строка и крайний левый столбец содержат коэффициенты при соответствующих неизвестных в целевой функции z.

Последняя строка называется оценочной, а элементы строки – оценками. Первый элемент а₀₀ оценочной строки представляет собой значение целевой функции z на начальном опорном плане:

= (0, 0, 45, 31, 30).

Это значение может быть получено как результат скалярного умножения вектора-столбца с_j на вектор-столбец свободных членов а_i0:

Оценки при неизвестных вычисляются по правилу: оценка при х_j равна сумме произведений элементов первого столбца на соответствующие элементы столбца x_j минус коэффициент с_j, записанный над столбцом х_j. Так оценка при х₁ равна:

Оценки при всех базисных неизвестных всегда равны нулю.

Составим симплексную таблицу.

cj	базис (xj)	аi0	7	5	0	0	0
			х1	х2	х3	х4	х5
0 0 0	x3 x4 x5	45 31 30	3 5 2	4 2 3	1 0 0	0 1 0	0 0 1	15 31/5 15
	z	0	-7	-5	0	0	0
0 7 0	x3 x1 x5	132/5 31/5 88/5	0 1 0	14/5 2/5 11/5	1 0 0	-3/5 1/5 -2/5	0 0 1	132/5 31/2 88/11
	z	217/5	0	–11/5	0	7/5	0
0 7 0	x3 x1 x2	4 3 8	0 1 0	0 0 1	1 0 0	–1/11 3/11 –2/11	–14/11 –2/11 5/11
	z	61	0	0	0	1	1

Исходное опорное решение

x₁ = (0, 0, 45, 31, 30), z₁ = 0

В оценочной строке две отрицательные оценки: –7, –5. Выбираем в качестве разрешающего столбец, соответствующий х₁, т.к. оценка этого столбца (–7) наименьшая отрицательная оценка. Разрешающая строка выбирается по этот минимум достигается для 2-й строки. Итак, в базис вводим х₁, выводим из базиса х₄. В результате первого шага получаем второе опорное решение

x₂ = .

После выполнения 2-го шага получаем оптимальное решение:

х_опт = (3, 8, 4, 0, 0), z_max = 61.

Дальнейшее увеличение z невозможно, т.к. все оценки стали неотрицательными.

Оптимальное решение исходной задачи получается отбрасыванием из компонент, связанных с балансовыми переменными х₃, х₄, х₅, т.е. х_опт = (3,8). При этом значение z_max не изменится.

Теперь дадим геометрическую интерпретацию задачи. Рассмотрим систему неравенств, определяющих множество допустимых планов:

Построим граничную прямую: 3х₁ + 4х₂ = 45

х1	0	45/3
х2	45/4	0

Прямая 3х₁ + 4х₂ = 45 разделила на две части (полуплоскости) плоскость ХОУ. Чтобы определить полуплоскость, точки которой удовлетворяют неравенству , достаточно проверить одну точку. Проще подставить точку с координатами (0,0). Получим верное неравенство: , следовательно, полуплоскость включает точку (0,0).

Определяем положение полуплоскостей, отвечающих каждому неравенству и находим пересечение этих полуплоскостей. Два последних условия в системе ограничений означают, что допустимые планы принадлежат неотрицательному квадрату (первой координатной четверти). Тем самым областью решения системы является четырехугольник ОАВС (Рис. 20).

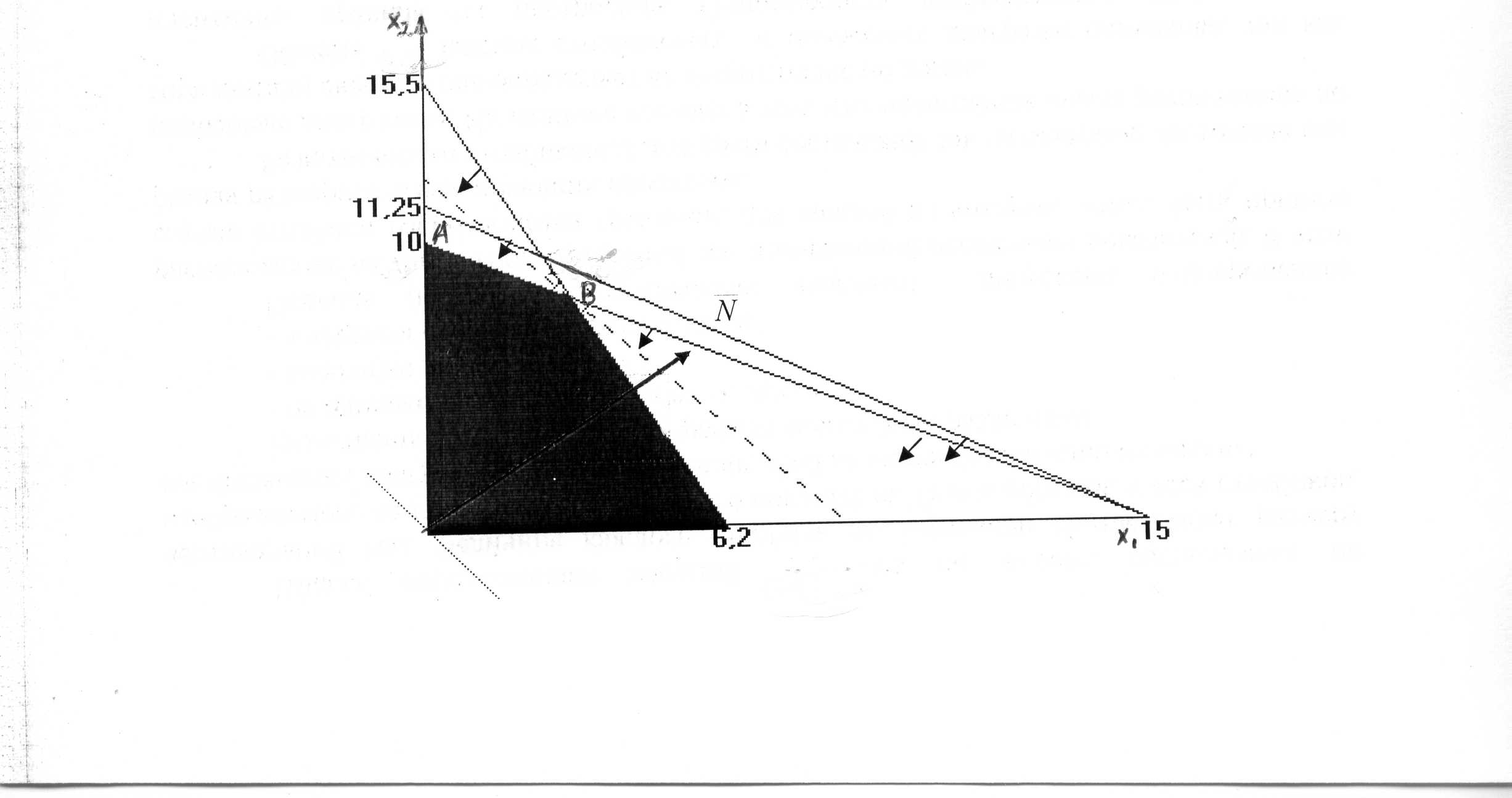
Рис. 20

Линии уровня целевой функции z задаются уравнением 7х₁ + 5х₂ – const. Легко видеть, что они образуют семейство параллельных прямых. Вектор = (7, 5) называется целевым, он перпендикулярен линиям уровня. Этот вектор указывает направление, двигаясь в котором, мы переходим от меньших значений z к большим, т.е. он указывает направление возрастания функции z. Вершина многоугольника, через которую проходит последняя линия уровня, даст наибольшее значение целевой функции. На рисунке видно, что максимальное значение будет достигнуто в вершине В. Найдем координаты точки В. Эта точка лежит на пересечении прямых 5х₁ + 2х₂ = 31, 2х₁ + 3х₂ = 30.

Решая систему из двух уравнений с двумя неизвестными, находим, что точка В имеет координаты х₁ = 3, х₂ = 8, .

Контрольные вопросы

1. Сформулируйте последовательность действий определяющих содержание процесса постановки задачи теории принятия решений.

2. Что называют критерием оптимальности модели?

3. Какую модель называют однокритериальной, многокритериальной?

4. Особенности построения оптимизационной модели линейного программирования.

5. Этапы решения задачи линейного программирования графическим и симплексным методом.

Задания

1. Требуется найти максимум функции L = x₁ + 4x₂, при ограничениях

Решите задачу графическим способом.

2. Требуется найти максимум функции при ограничениях

3. На предприятии, в состав которого входят 4 производственных цеха, изготавливаются два вида изделий А и В. Производственные мощности цехов (в часах) в расчете на сутки, нормы времени, необходимого для изготовления единицы изделия А и В в соответствующих цехах, приведены в таблице.

Цех	Изделия		Производственные мощности
	А	В
1	2	2	12
2	1	2	8
3	4	0	16
4	0	4	12

Прибыль от продажи единицы изделия А составляет 2 д.е., а от продажи единицы изделия В – 3 д.е. Следует выбрать тот из возможных вариантов производственного плана, при котором обеспечивается максимальная прибыль.

Мы ограничились построением математической модели и решением в рамках модели задачи линейного программирования на нахождения максимального значения функции при заданных ограничениях. В теории линейного программирования рассматривается также постановка и решение задач на поиск минимального значения целевой функции, построение двойственной задачи, частные случаи задачи. Эти вопросы изложены в литературе, библиографический список которой приведен в конце учебника.