Используя необходимые условия экстремума функции нескольких переменных, получаем следующую систему уравнений для определения неизвестных параметров:

Рассмотрим применение метода наименьших квадратов к нахождению коэффициентов функций.

1) Если эмпирическая функция имеет вид , то функция в этом случае имеет вид .

Эта функция с двумя переменными а и ( и - экспериментальные данные из таблицы). Используя необходимые условия экстремума, перейдем к системе:

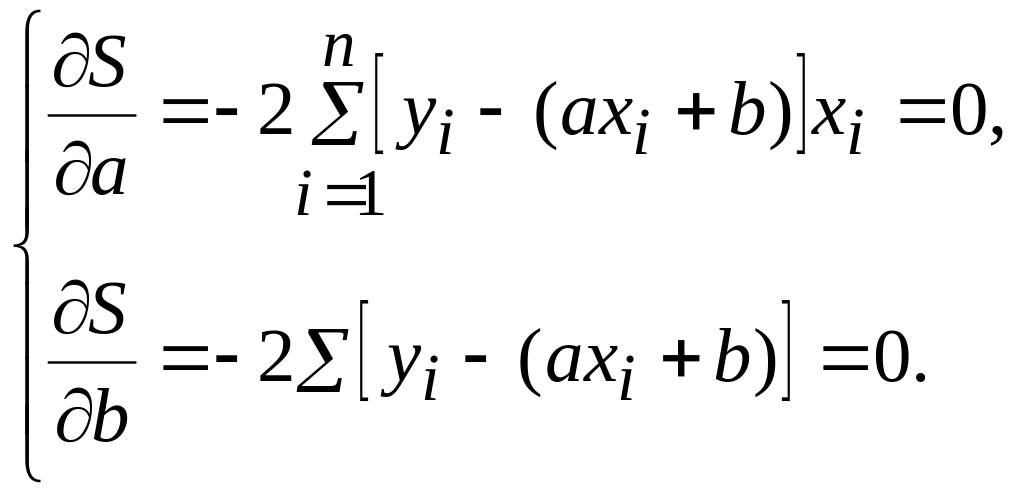
После преобразований получим систему двух линейных уравнений с двумя неизвестными, называемую нормальной системой для определения параметров а и :

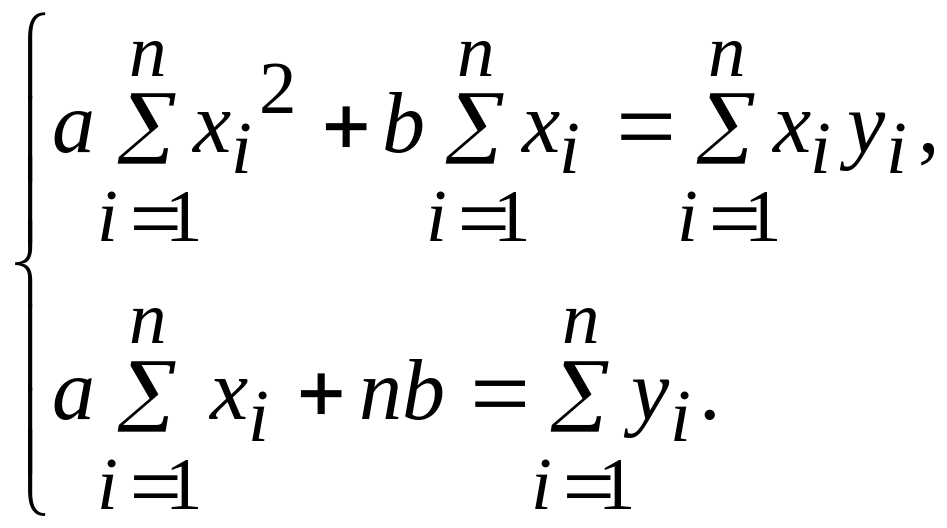
После решения системы, найденные значения параметров а и подставим в аппроксимирующую функцию .

Пример. В результате некоторого эксперимента получены пары значений переменных X и Y:

X	2	4	6	8	10
Y	5.5	8.5	13.6	17.3	20.1

Методом наименьших квадратов найти аппроксимирующую функцию вида .

Очевидно, что точки с данными координатами не могут быть расположены на одной прямой, нужно построить прямую, “сглаживающую” эти точки. В нашем случае n = 5. Нормальная система для определения параметров а и в случае линейной зависимости имеет вид:

Составим вспомогательную таблицу для подсчета коэффициентов системы:

2	4	5.5	11
4	16	8,5	34
6	36	13,6	81,6
7	64	17,3	133,4
10	100	20,1	201
∑= 30	220	65	466

Таким образом, , =220, , . Подставляя эти значения в нормальную систему, получим:

а = 1,9; =1,6.

Искомая зависимость между переменными х и у выражается формулой .

2) Пусть аппроксимирующая функция является квадратичной и имеет вид

Функция в данном случае имеет вид

и принимает минимальное значение при тех значениях и с, при которых обращаются в нуль частные производные этой функции по каждой переменной: .

Находя указанные частные производные, после упрощений получим следующую нормальную систему для нахождения параметров и с:

3) Пусть экспериментальным значениям соответствует показательная функция . Логарифмируя левую и правую части равенства, получим . Введем подстановку , .

Полученная функция является линейной.

Выразим а, b: .

Принцип наименьших квадратов позволяет найти наилучшую модель идентификации для исследуемой экспериментальной выборки с заданным уравнением регрессии.

Определен ряд требований, обеспечивающих корректность применения регрессионного анализа для построения стохастических моделей [11].

1. Независимость наблюдений.

Результаты отдельных измерений – независимые случайные величины. Это означает, что отклонения от закономерностей, полученные в одних опытах, не оказывают влияния на подобные отклонения в других.

2. Одинаковая распределенность случайной ошибки наблюдений .

Значение отклика y можно мысленно разделить на две составляющие:

, где является функцией факторов, случайная, по отношению к ним, величина с нулевым математическим ожиданием.

Если понимать как ошибку измерения отклика, то измерения отклика имеют равную точность при всех значениях факторов. Если понимать как внутренне присущую отклику изменчивость, то эта изменчивость не испытывает влияния со стороны факторов. имеет неизменную статистическую природу во всех опытах.

3. Предположение о форме регрессионной зависимости.

Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости. Например, одинаковыми по форме являются корреляционные зависимости возраста учеников средней школы от года их обучения в школе и возраст студентов высшего учебного заведения от года обучения. Но зависимость возраста учеников средней школы от года их обучения в школе является более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возрасте, чем у школьников, обучающихся в одном классе. Показателем связи между исследуемыми величинами (факторами о откликами) является коэффициент корреляции.