3.4. Корреляционно-регрессионный анализ как метод выбора оптимальной математической модели

В корреляционно-регрессионном анализе выделены две составляющие части – корреляционный анализ и регрессионный анализ. Корреляционный анализ – это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ – это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Предположим, что исследуются параметры X и Y наблюдаемого признака генеральной совокупности по данным выборочной модели.

Эти значения являются случайными величинами с соответствующими распределениями. Если зафиксировать некоторое значение случайной величины Х (значение х), то переменная Y , в силу ее стохастической зависимости от Х, может принимать любое значение из некоторого множества значений. Среднее арифметическое этих значений называют условным средним значением параметра y, при условии, что и обозначают . Аналогично определяется условное среднее .

Зависимость условного среднего от значений величины х (или от y) является функциональной и называется корреляционной зависимостью.

При статистических исследованиях корреляционных зависимостей одной из главных задач является определение формы корреляционной зависимости, т.е. построение модели связи.

Выделяют ряд характеристик, ориентируясь на которые различают виды корреляционных зависимостей.

1) По форме корреляционные зависимости бывают линейные и нелинейные. Например, зависимость покупаемости товара и количества предъявлений его рекламы представляет собой нелинейную корреляцию (Рис. 15).

Рис. 15

2) По направлению связи различают прямую и обратную корреляции. При прямом направлении корреляции усилению (увеличению) одного признака (фактора) соответствует усиление (увеличение) другого (отклика) и ослабление (уменьшение) – при обратном. На рисунке 16 изображено корреляционное поле прямой корреляции

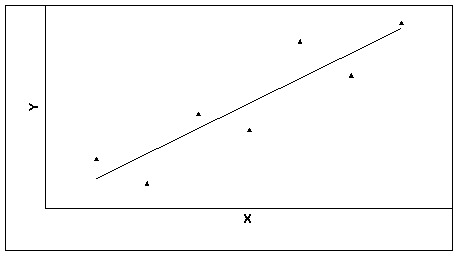
Рис. 16

3) По количеству признаков – парная и множественная. Корреляция называется парной, если связаны между собой два каких-либо признака. Если изучается связь одного признака с несколькими (хотя бы с двумя) другими, рассматриваемыми в совокупности, то корреляция называется множественной. Выделяют также частную корреляцию, при которой изучается связь между некоторым отдельным признаком и одним из признаков совокупности при фиксированных значениях остальных признаков этой совокупности.

4) По силе (сила связи не зависит от направления связи) корреляция характеризуется абсолютной величиной коэффициента корреляции r. При r = 1 наблюдается жесткая положительная связь, то есть при увеличении значений одного признака обязательно увеличение значений другого; при значении r = -1 – гарантированное уменьшение; при значении r = 0 – изменение значений одного никоим образом не повлечет за собой изменения другого.

Классификация корреляционных связей по степени силы.

а) общая классификация:

Характеристика силы корреляции	Значение абсолютной величины коэффициента корреляции ( )
Сильная или тесная	более 0,70
Средняя	от 0,50 до 0,69
Умеренная	от 0,30 до 0,49
Слабая	от 0,20 до 0,29
Очень слабая	меньше 0,19

б) частная:

Высокая значимая корреляция	при r, соответствующем уровню статистической значимости
Значимая корреляция	при r, соответствующем уровню статистической значимости
Тенденция достоверной связи	при r, соответствующем уровню статистической значимости
Незначимая корреляция	при r, не достигающем уровня статистической значимости.

Первая из классификаций ориентирована только на величину коэффициента корреляции, а вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньшей величины коэффициента корреляции оказывается достаточно для того, чтобы корреляция была признана достоверной. В результате, при малом объеме выборки и сильная корреляция может оказаться недостоверной (что объясняется большой возможностью обнаружения случайных связей). В то же время, при больших объемах выборки даже слабая корреляция между какими либо признаками может оказаться достоверной.

Для аналитических целей корреляционную зависимость представляют при помощи математических функций, т.е. придают ей функциональную форму ( ). Под формой связи понимают тенденцию, которая проявляется в изменении результативного признака в связи с изменением признака-фактора.

Форма корреляционной связи может быть выражена различными математическими функциями. Выбор формы связи решается на основе теоретического анализа изучаемых явлений и исследования эмпирических данных. Линейная форма связи может быть выражена уравнением прямой (Рис. 17):

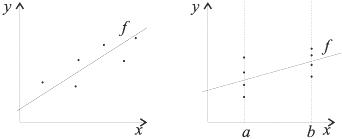
Рис.17

Нелинейная форма связи может быть выражена уравнениями:

уравнением параболы ;

уравнением гиперболы ;

показательной функцией ;

степенной функцией

и другими функциями.

Главной проблемой при построении модели связи является определение вида аналитической функции, отражающей механизм связи между факторным и результативным признаками и позволяющей дать количественную оценку этой связи.

Уравнение связи ( ) называется модельным уравнением регрессии (или уравнением регрессии), график – линия регрессии, а анализ, производимый с помощью уравнения регрессии, называется регрессионным анализом. Уравнение регрессии является статистической моделью связи между исследуемыми признаками.

Корреляционная зависимость между исследуемыми параметрами Х и Y называется линейной корреляцией, если обе функции регрессии и являются линейными. В этом случае обе линии регрессии являются прямыми, они называется прямыми регрессии.

Эмпирическое исследование формы связи включает построение графиков корреляционных полей, эмпирических линий регрессии, а также анализ параллельных рядов. Изучение эмпирического материала дает возможность установить направление и форму связи.

После установления вида функции для модели связи определяются параметры а и b уравнения регрессии. Параметры уравнения регрессии определяются методом наименьших квадратов. Рассмотрим теоретические основы метода.

Пусть требуется установить зависимость между двумя величинами и , при условии проведения наблюдений. Результаты наблюдений внесены в таблицу:

			…
			…

Предположим, что табличным значениям переменных соответствует эмпирическая функция . Рассмотрим сумму квадратов разностей значений , полученных экспериментально, и значений функции в соответствующих точках:

,

здесь - квадрат отклонения ординаты функции в точке от экспериментальной ординаты данной точки. Подберем параметры такими, чтобы сумма имела наименьшее значение: