
- •111900.68 – Ветеринарно-санитарная экспертиза
- •Оглавление
- •Предисловие
- •Введение
- •В результате изучения дисциплины «Математическое моделирование» магистранты должны:
- •1. Основы математического моделирования
- •1.1. Понятие математической модели
- •1.2. Основные этапы математического моделирования
- •1.3. Классификации математических моделей
- •1.4. Графическое представление математических моделей
- •1.5. Основные методы построения математических моделей
- •2. Теоретические основы построения стохастических моделей
- •2.1. Случайные величины. Основные виды случайных величин
- •2.2.Числовые характеристики случайных величин
- •Стохастические модели и их виды
- •3. Выборочный метод. Построение модели выборки
- •3.1. Основные понятия выборочного метода
- •3.2. Статистические оценки параметров генеральной совокупности
- •Точечные оценки параметров генеральной совокупности.
- •3.3. Статистические методы проверки адекватности математических моделей
- •3.4. Корреляционно-регрессионный анализ как метод выбора оптимальной математической модели
- •Используя необходимые условия экстремума функции нескольких переменных, получаем следующую систему уравнений для определения неизвестных параметров:
- •Рассмотрим применение метода наименьших квадратов к нахождению коэффициентов функций.
- •После решения системы, найденные значения параметров а и подставим в аппроксимирующую функцию .
- •3.5. Коэффициент корреляции
- •4. Математические модели теории принятия решений
- •4.1. Общие сведения о теории принятия решений
- •4.2. Понятие оптимизационной математической модели
- •4.3. Оптимизационная модель задачи линейного программирования
- •4.4. Решение задачи линейного программирования в рамках построенной модели
- •Заключение
- •Ответы к заданиям
- •Приложения Приложение 1.
- •Приложение 2
- •Библиографический список
3.2. Статистические оценки параметров генеральной совокупности
При обработке наблюдений редко приходится прибегать к построению эмпирической функций распределения. Анализ условий испытаний позволяет предварительно определить тип неизвестной функций распределения – биноминальное, нормальное, равномерное и др. И окончательное уточнение неизвестной функции распределения сводится к определению некоторых числовых параметров генеральной совокупности. Эти параметры определяются приближенно по выборочной модели.
Допустим, что закон
распределения генеральной совокупности
случайной величины содержит неизвестный
параметр
![]() . Требуется
с помощью выборки
. Требуется
с помощью выборки
![]() найти оценку
найти оценку
![]()
![]() этого
параметра. Очевидно,
является
случайной величиной. Для того чтобы эта
оценка имела практическую ценность,
необходимо, чтобы она обладала рядом
свойств.
этого
параметра. Очевидно,
является
случайной величиной. Для того чтобы эта
оценка имела практическую ценность,
необходимо, чтобы она обладала рядом
свойств.
1. Свойство несмещённости.
Математическое
ожидание оценки должно совпадать со
значением оцениваемого параметра
![]() при любом объеме выборки. Это означает
отсутствие систематической ошибки
одного знака (в сторону занижения:
при любом объеме выборки. Это означает
отсутствие систематической ошибки
одного знака (в сторону занижения:
![]() ,
в сторону завышения:
,
в сторону завышения:
![]() ).
).
2. Свойство состоятельности.
Оценка должна с
увеличением объема выборки по
вероятности стремиться к оцениваемому
параметру, т.е.
![]() ,
,
![]() .
.
Это означает, что
с увеличением объема выборки практически
достоверно, что
![]() .
Свойство состоятельности обязательно
для любого правила оценивания, иначе
она не имеет практического смысла, т.к.
увеличение объема исходной информации
не будет приближать к истине.
.
Свойство состоятельности обязательно
для любого правила оценивания, иначе
она не имеет практического смысла, т.к.
увеличение объема исходной информации
не будет приближать к истине.
3. Свойство эффективности.
Для того чтобы несмещенная оценка параметра была эффективной она должна иметь минимальную дисперсию среди всех несмещенных оценок этого параметра.
Точечные оценки параметров генеральной совокупности.
Несмещенной и состоятельной оценкой математического ожидания генеральной совокупности – генерального среднего
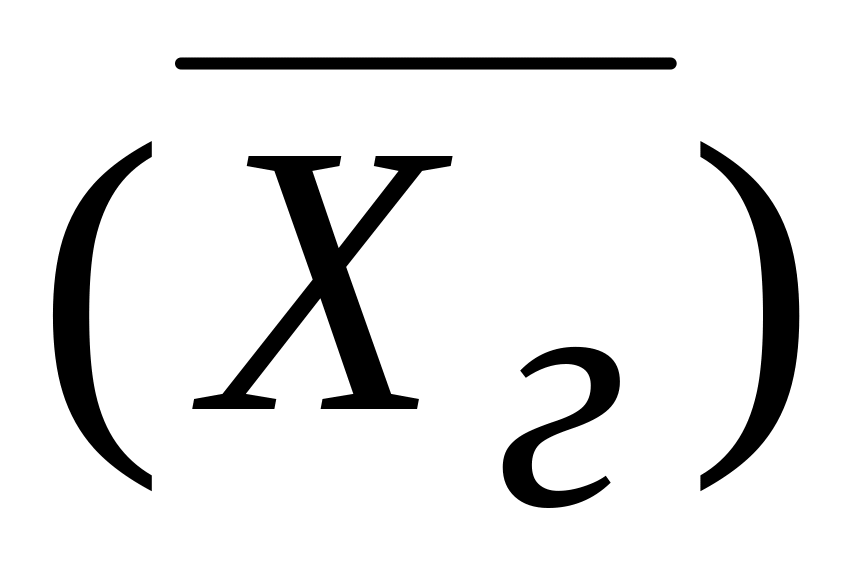 является
выборочное
среднее
является
выборочное
среднее
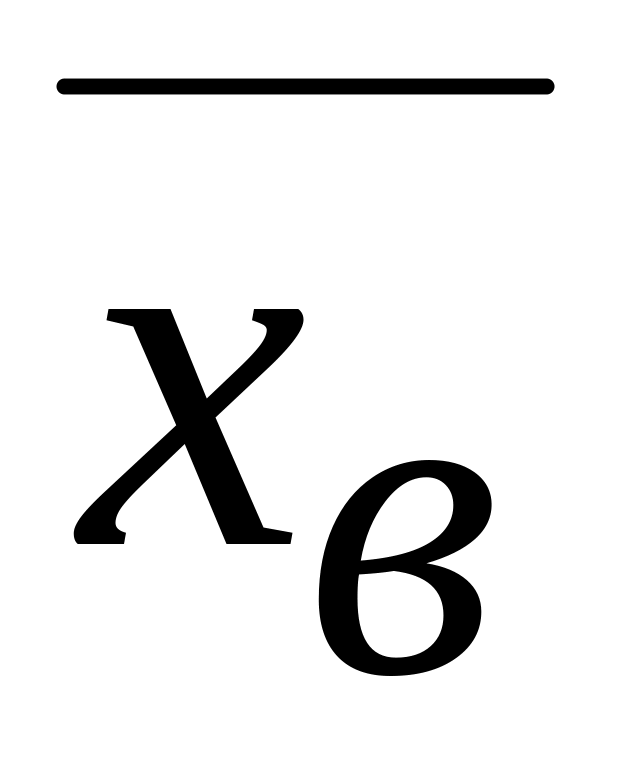 :
:
 .
.
В случае нормального распределения Х эта оценка является эффективной.
Несмещенной и состоятельной оценкой генеральной дисперсии S2 является исправленная выборочная дисперсия:

II. Интервальные оценки параметров генеральной совокупности.
Точечные оценки могут быть приняты в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестна точность, с которой они оценивают параметр. Все точечные оценки параметров распределения генеральной совокупности вычисляется по выборкам, но из-за случайности выборок оценки является случайными величинами, которые могут отличаться от постоянного истинного значения параметра.
Если при большом числе опытов точечная оценка (в силу несмещённости, состоятельности и эффективности) близка к неизвестному параметру, то для выборок небольшого объема вопрос о точности существен.
Пусть - неизвестный параметр распределения и - его оценка.
Величина
![]() называется точностью оценки. Зададим
малое положительное число
называется точностью оценки. Зададим
малое положительное число
![]() и условимся, чтобы
и условимся, чтобы
![]() .
Нельзя наверняка утверждать, что это
равенство всегда выполняется, т.к.
.
Нельзя наверняка утверждать, что это
равенство всегда выполняется, т.к.
![]() случайная
величина. Можно лишь задать некоторую
вероятность
случайная
величина. Можно лишь задать некоторую
вероятность
![]() (надежность оценки), с которой это
неравенство выполняется, т.е.
(надежность оценки), с которой это
неравенство выполняется, т.е.
![]() .
.
Интервал
![]() называется доверительным
интервалом,
покрывающим оцениваемый параметр
с вероятностью
. Величину
выбирают близкой к единице: 0,95; 0,99; 0,999.
Событие, состоящее в том, что доверительный
интервал
называется доверительным
интервалом,
покрывающим оцениваемый параметр
с вероятностью
. Величину
выбирают близкой к единице: 0,95; 0,99; 0,999.
Событие, состоящее в том, что доверительный
интервал
![]() ,
где
,
где
![]() ,
,
![]() ,
накроет исследуемый параметрм –
практически достоверное, а границы
,
накроет исследуемый параметрм –
практически достоверное, а границы
![]() симметричны относительно соответствующее
точечной оценки.
симметричны относительно соответствующее
точечной оценки.
Доверительный интервал для математического ожидания нормально распределенного признака генеральной совокупности:
 ,
где
,
где
 выборочное
чсреднее,
выборочное
чсреднее,
 среднее
квадратичное отклонение наблюдаемого
признака генеральной совокупности, n
– объем выборки, величину t
находят из условия:
среднее
квадратичное отклонение наблюдаемого
признака генеральной совокупности, n
– объем выборки, величину t
находят из условия:
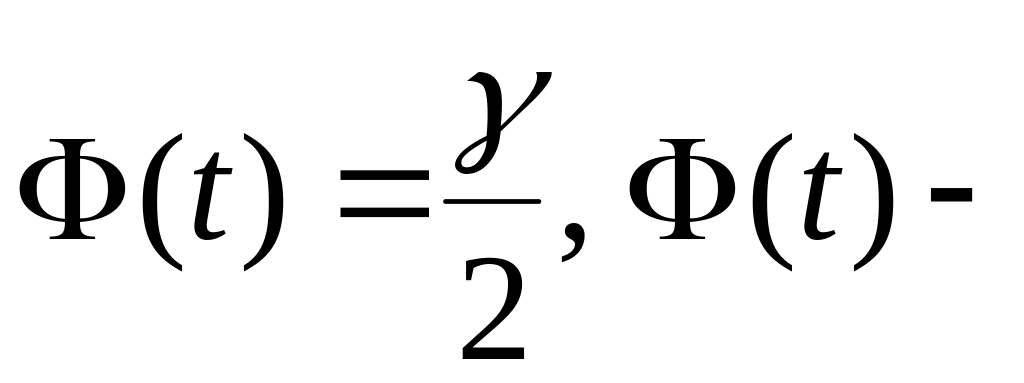 значение
интегральной функции Лапласа, по этому
значению функции из таблиц выбирают
t.
значение
интегральной функции Лапласа, по этому
значению функции из таблиц выбирают
t.
Если
среднее квадратичное отклонение
наблюдаемого признака генеральной
совокупности
![]() неизвестно, то доверительный интервал:
неизвестно, то доверительный интервал:
![]() ,
где
,
где
![]() ,
,
![]() квантиль
уровня
квантиль
уровня
![]() ,
значения
,
значения
![]() выбирают из таблиц квантилей распределения
Стьюдента.
выбирают из таблиц квантилей распределения
Стьюдента.
При n>30 числа t и , найденные по таблицам, практически совпадают.
2)
Доверительный интервал для среднего
квадратического отклонения
![]() нормально
распределенного признака генеральной
совокупности
по исправленному выборочному среднему
квадратичному отклонению
нормально
распределенного признака генеральной
совокупности
по исправленному выборочному среднему
квадратичному отклонению
![]() :
:
![]() ,
при
,
при
![]() ;
;
![]() при
при
![]() ;
;
![]() – выбирают из таблиц.
– выбирают из таблиц.
Замечание. В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратичного отклонения случайных ошибок измерений. Так как обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то вопрос о нахождении точности прибора с надежностью сводится к нахождению доверительного интервала, покрывающего c заданной надежностью .
