Другая формулировка теоремы Котельникова (критерий Найквиста)

Любая функция с ограниченным спектром может быть восстановлена с некоторой точностью (в зависимости от типа ФНЧ), если f_д не менее чем в 2 раза превосходит f спектра.

В самой теореме утверждается, с помощью какого фильтра это можно сделать:

; здесь – выборки.

Особые случаи дискретизации

1. Субдискретизация (UnderSampling):

f_д может быть в сотни раз меньше, чем по Котельникову в ряде специальных случаев.

Дискретизация сигналов с компактным спектром

Теорему Котельникова можно не рассматривать, когда спектр компактный.

До сих пор мы не имели дело с сигналами около нуля (в основной полосе частот). Но бывает (например в стандарте GSM):

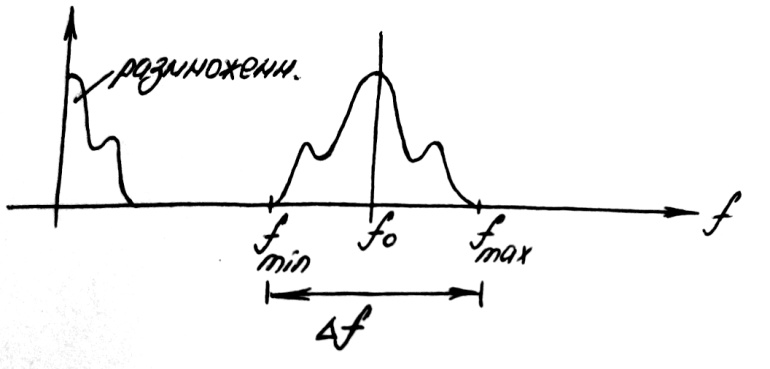
Размножая спектр с точки зрения восстановления сигнала, нет разницы с сигналом из ОПЧ.

Функцию размножения сигнала выполняет АЦП.

Критерий в данном случае: для сигнала с компактным спектром частота дискретизации должна больше, чем в 2 раза, превосходить ширину спектра сигнала. (Радиосигнал), .

Какими свойствами должен обладать АЦП: существуют 2 класса, это

– найквистовские АЦП, и

– АЦП для субдискретизации.

2. Избыточная дискретизация (передискретизация):

(в 32, 64 и иногда больше раз выше).

Это позволяет повысить точность АЦП.

3. Стробоскопическая дискретизация.

Семинар№3

Рассмотрим:

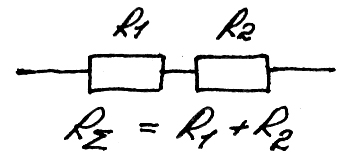
Очевидно, что, чтобы получить большое выходное, сопротивление, нужно подключить параллельно :

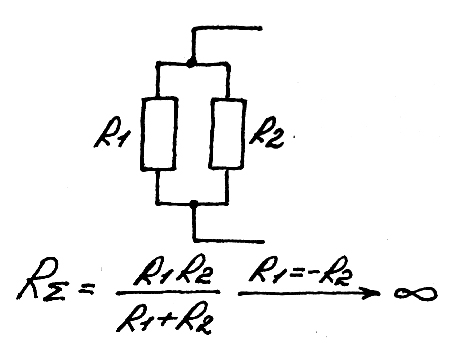
Есть схемы с отрицательным сопротивлением – триггеры, бистабильные ячейки.

Шум конденсатора

Шум возникает из-за разбаланса носителей (происходит хаотическая перезарядка).

(двойная амплитуда ),

при С = 1пФ, Т = 300 К.

На высоких частотах конденсатор превращается в резистор.

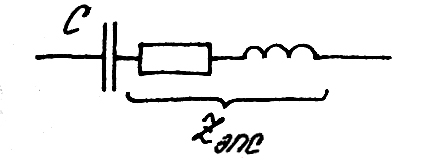
Диэлектрическая адсорбция, .

Реальная схема:

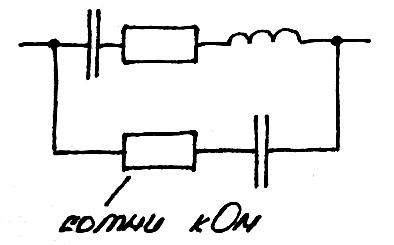
Внутренний конденсатор не разряжается до конца долгое время. Такой принцип используется при создании электромагнитного оружия.

Диоды

Существуют различные виды диодов:

Схемы диодного включения:

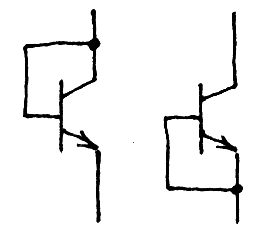
Материалы для изготовления диодов – кремний, карбид кремния.

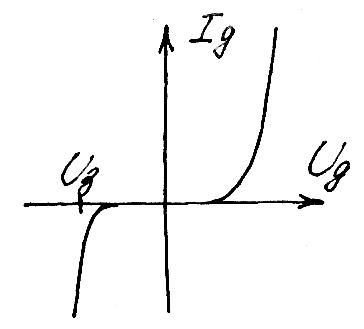
ВАХ диода:

Uз. – напряжение пробоя (зейнеровский туннельный ~ 0.5 В, лавинный ~ 7 В).

Определим рабочую точку на схеме:

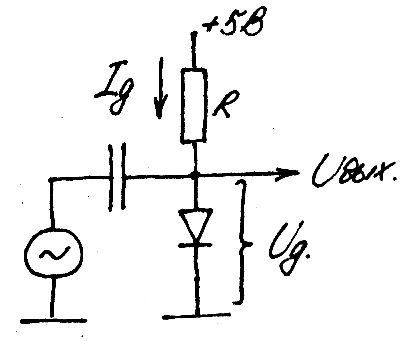
m = 1

I₀ = 10 fA

R = 1 kОм

Ток Iд. не обязательно считать с большой точностью, т.к. он находится под Епит.

; возьмём U* = 0.7 В, тогда .

Далее, , что приблизительно соответствует диоду Шотки.

Проведём коррекцию: U* = 0.4 В, тогда Iд. = 4.6 мА, Uд. = 275 ln 4.6 = 420 мВ.

В итоге, рабочая точка: Uвых. = 0.42 В;

Iд. = 4.6 мА.

Рассмотрим такую схему:

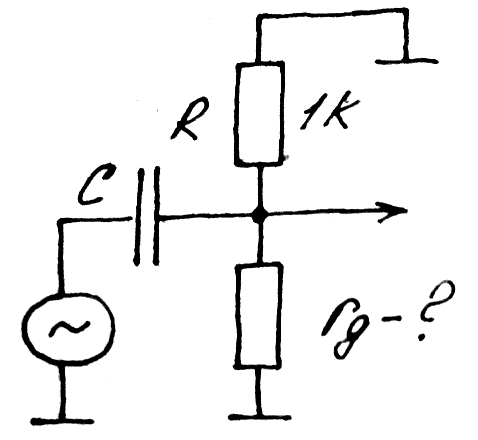
Здесь ; .

Эквивалентная схема для малого сигнала (если при воздействии сигнала рабочая точка практически не меняется, то это РМС):

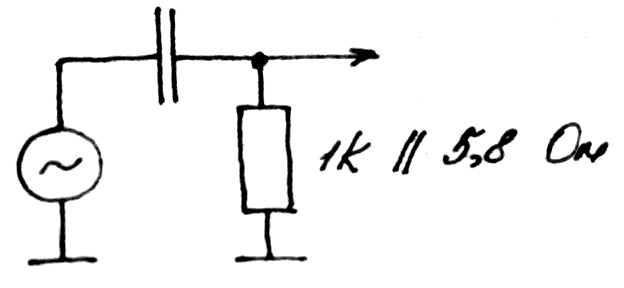
Лекция 4

Стробоскопические преобразование

Применяются только для периодических сигналов! Сигнал периодический → спектр линейчатый.

Tc

Tд

Tк

t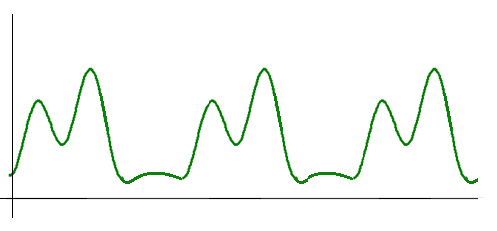

.

F1

F0

2F1

F

Fд=

Рис.4.1 Стробоскопическое преобразование

Период дискретизации намного больше периода сигнала.

П оследовательные точки в разных периодах. Поэтому, обходя теорему Котельникова, резко уменьшаем частоту дискретизации. Спектр сворачивается по частоте дискретизации.

Вопрос на экзамене: Необходимо показать, что путем трансляции из дальних частот Найквиста при наложении не будет расходимости.

Тд>T →fд<fc → спектр дискретного сигнала.

S(t) – спектр сигнала, расстояние между отсчетами

После того, как сигнал размножили, необходимо транслировать. А затем перетранслировать. Если не учитывать инверсию, то получится то же, что и в начале.

Задача(shift mind):

Восстановить синусоидальный сигнал υ(sin)=660кГц по выборкам υ_д=1мГц. Какой частоты будет восстановленный сигнал?

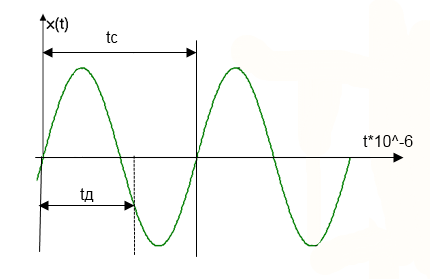
Рис 4.2 Синусоидальный сигнал

Р

S(t)

S(f)

ешение:

t

f

0

0

W(t)

W(f)

t

f

T/2

-T/2

S(t)*W(t)

S(f)*W(f)

c(t)

c(f)

t

f

t

f

S(t)*W(t)*c(t)

S(f)*W(f)*c(f)

t

f

Рис 4.3 Восстановление сигнала по дискретным выборкам.