НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»

Факультет Автоматики и электроники Кафедра №27 Микро- и наноэлектроники

Лекции по курсу

МИКРОСХЕМОТЕХНИКА часть II

Москва 2011 г.

Лекция №1

Предмет курса «Аналоговая схемотехника».

Аналоговый сигнал (величина) – это такая величина, которая является вторичной производной по отношению к первичной физической величине и выражению в уровнях тока и напряжения.

Весь окружающий нас мир аналоговый. Аналоговая величина не обязательно должна быть непрерывной. Непрерывная величина – это математическое понятие. Применительно к сигналу она может быть непрерывна по значению (в заданном диапазоне может быть измерена с любой точностью) и по времени (в заданном диапазоне можно сказать, что точка, в которой определено значение величины находится в строго определённый момент времени).

Сигнал – это информационное сообщение, развёрнутое во времени.

Раньше были аналоговые системы связи (каналы связи). Для них скорость передачи сигнала определяется по формуле:

где - мощность сигнала, а - мощность шума.

Э та система основана на канале без памяти. Скорость передачи для таких систем очень низкая. Чтобы её повысить сейчас начали использовать модемы, основанные на каналах с памятью.

С ейчас используются цифровые системы связи:

Кодеры – это процессоры, которые содержат порядка 1 млн транзисторов. Умножители тоже очень большие элементы. Это схема устройства мобильного телефона GSM.

О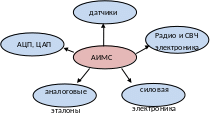 бласти применения АИМС.

Элементная база АИМС.

В природе не существует источников. Источники тока и напряжения, которые используются при расчётах схем – это математические понятия.

Источники сигналов.

И сточник напряжения – это такой источник, чьим сопротивлением в данной цепи можно пренебречь.

И

I

сточник тока – это такой источник, чьё внутреннее сопротивление в предельной схеме можно считать бесконечным, то есть ток в нагрузке мало зависит от её номинала.

О дним из основных тождеств при расчёте схем является следующее – источник напряжения, соединённый последовательно с нагрузкой можно заменить на источник тока, соединённый с этой же нагрузкой параллельно.

r

r

Земля.

В печатных платах есть много разных земель. И обозначаются она по-разному.

– корпус прибора

– физическое заземление (точка с нулевым потенциалом)

и т.д. – общий провод (на схемах для удобства общие провода обозначаются одним из подобных символов, что упрощает чтение схемы)

Чувствительность.

Функция чувствительности показывает относительное изменение одного параметра по отношению к относительному изменению другого параметра.

Р

Е

U_н

ассмотрим пример. Возьмём делитель напряжения.

R₁

R₂

Л инейные резисторы.

Шум.

Любая резистивность шумит:

[В_скв]

Шум измеряется в среднеквадратичных вольтах.

- время наблюдения случайного процесса.

Рассмотрим междупиковый шум. Пусть доверительная вероятность =2σ, то есть говорят, что весь основной процесс укладывается в 2σ. Тогда вероятность = 32%. Если взять доверительную вероятность = 4σ, то вероятность окажется = 4%. Аналогично 6σ соответствует вероятности 0,27%; 6,6σ – 0, 1%; а 10σ – 0,00006%.

Обычно указывается спектральная плотность мощности шума:

[ ]

Если спектральная плотность шума = 0, 7 – то это очень хорошо; если 3 – 4, то хорошо, а если больше 20, то плохо.

Лекция№2

Математический этюд 1.

δ-функция.

К онкретный вид функции нас не интересует. δ-функция определяется так:

δ(х)=0, если х≠0 δ(х)→∞, еслт х=0

Отсюда следует единственное полезное свойство δ-функции – стробирующее (фильтрующее) свойство:

Интеграл несобственный, то есть не в понимании Коши/Римана/Гаусса, а является функционалом, то есть ставится в соответствие число к функции. Мы должны знать мгновенное значение сигнала в какой-то момент времени. Его вырезает δ-функция.

δ-функция – это производная единичного скачка:

δ(х)=e’(x) e(t)=

Другой вариант определения δ-функции:

Е щё одно важное соотношение:

Сигнал.

Сигнал имеет две формы представления:

• временная область

• частотная область

Рассмотрим их взаимосвязь:

Спектр периодической функции всегда имеет вид u(t)=u(t+T), где Т называют периодом функции. Рассмотрим ряд Фурье для такой функции:

– средняя по времени постоянная составляющая сигнала

nω₁ - гармоники; – первая (фундаментальная) гармоника

Р ассмотрим пример.

Т

- скважность

Если в одной области сигнал прямоугольный, то в другой он будет определяться, как .

Если у нас меандр, то есть τ=Т/2, то u(t)=A*[1/2+2/π*(cosω₁t+1/3 cos3ω₁t+1/5 cos5ω₁t+…]. Удобно использовать отрицательные частоты, чтобы было видно всю картину. Это нужно для анализа. Физически же отрицательные частоты отсекаются.

Спектр линейчатый. Период огибающей связан с иголками. Расстояние между ними связано с периодом следующим образом – если он маленький, иголки находятся далеко друг от друга, а если период большой, то спектр почти сплошной. Отсюда вытекает следующее правило:

Чем более детально мы хотим описать сигнал, тем дольше мы должны его наблюдать.

Для наблюдения спектра сигнала можно использовать осциллограф, а можно спектроанализатор, но это очень дорогой прибор.

Основы теории сигналов.

Геометрическое представление сигналов.

В ряде случаев множество сигналов можно рассматривать как линейное векторное пространство. В нём можно выделить подмножества, которые играют роль координатного базиса:

, где a_i – линейно независимы.

в этом случае любой сигнал можно будет разложить в этом базисе.

Если сигналы вещественные, то они имеют норму:

, E=||S||² - энергия сигнала.

Норма разности определяется так:

Скалярное произведение: .

Периодических сигналов в природе очень мало. В общем случае они непериодические. Они тоже представляются в пространстве частот. Тут уже нужны преобразования Фурье.

- прямое преобразование Фурье

- обратное преобразование Фурье

В разных источниках эти формулы иногда различаются на 2π.

Рассмотрим пример.

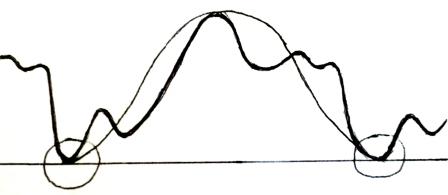
Есть одиночный сигнал. Если его продолжить аналитически вправо и влево, то получится ряд, то есть появится возможность использовать преобразования Фурье. Проблемы могут возникнуть при сшивке. В идеальном случае нужно, чтобы как можно больше производных было равно нулю. А у нас появляется скачок, который называется явлением Гиббса. Его убирают с помощью оконных функций. Окно – это функция вида Гауссовского колокола, которая позволяет обрезать резкие спады. Окон везде очень много, надо выбирать оптимальные.

Задача на дом

Найти такое А, чтобы расстояние между прямоугольным и синусоидальным сигналами было минимально.

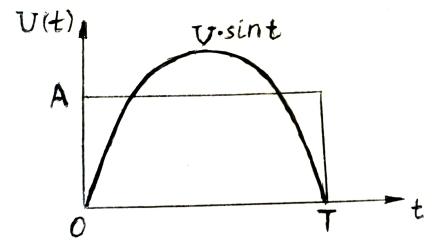Решение:

Так как в первом слагаемом отсутствует А, то его можно не рассматривать.

Чтобы расстояние было минимальным, необходимо найти минимум этой функции:

Математический этюд №2.

Корреляционная функция.

- корреляционная функция

- взаимокорреляционная функция

О ни используются в радиолокации. Посылается импульс, отражается и принимается. В идеальном случае должна получиться такая картинка:

А на деле получается что-то подобное:

Функция корреляции ищет сигнал, похожий на первоначальный. По её величине можно судить о похожести кусков. В максимумах они совпадают лучше всего.

Свёртка.

Свёрткой двух сигналов называется функция вида:

Очень важное математическое понятие. Если имеются две функции , то если во временной области, то тогда в частотной области . И наоборот, если в частотной области , тогда во временной

Спектр случайных сигналов. Теорема Виннера-Хинчена.

- прямое преобразование

– обратное преобразование

Это спектр мощности сигнала. По этому спектру мы восстанавливаем не сам сигнал (ведь он случайный), а его корреляционную функцию, то есть одну из его возможных форм.

Лекция№3

Формула Рэлея:

функции от времени (u, v) = (U, V) их спектры

Переход от аналоговых схем к цифровым происходит в три этапа:

– дискретизация,

– квантование,

– кодирование.