1. 7. Пересечение топографической поверхности с плос­костью, прямой, конической и цилиндрической поверхностями

1.7.1. Пересечение топографической поверхности с плоскостью и прямой

На рис. 29 заданы топографическая поверхность (горизонта­лями) и плоскость Р (масштабом уклонов Р,).

Для определения линии пересечения плоскости Р с топографической поверхностью отмечаем точки пересечения горизонталей плоскости и топографической поверхности, имеющих одинаковые отметки. Соединяя между собой последовательно найденные точки а₁₀, b₁₁, с₁₂ и др., полу­чим искомую проекцию линии пересечения.

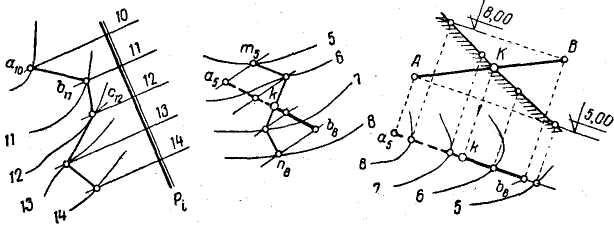
Рис. 29 Рис. 30 Рис. 31

При решении задачи на определение точки пересечения прямой с топографической поверхностью через прямую следует провести вспомогательную плоскость и определить линию пересечения этой плоскости с топографической поверхностью. Так, для определения точки пересечения прямой А₅В8 с заданной топографической поверх­ностью (рис. 30) проводим через предварительно проградуированную прямую такую вспомогательную плоскость, горизонтали кото­рой пересекаются с соответствующими горизонталями топографи­ческой поверхности в пределах чертежа.

Построив проекцию т₅п₈ линии пересечения вспомогательной Плоскости с топографической поверхностью, определяем в пересечении ее с проекцией а₅b₈ прямой проекцию искомой точки k.

На рис. 31 аналогичная задача решена с использованием вер­тикальной плоскости в качестве вспомогательной. В этом случае необходимо построить во вспомогательной плоскости, совмещенной с плоскостью чертежа, профиль рельефа топографической поверх­ности и прямую АВ. Точка К определяет положение искомой проек­ции k — проекции точки встречи прямой с топографической по­верхностью.

1.7.2. Пересечение топографической поверхности с конической поверхностью

Пусть поверхность прямого кругового конуса задана вершиной S₁₂ и горизонталью с отметкой 11 (рис. 32). Требуется определить линию пересечения конической поверхности с топографической поверхностью, заданной горизонталями 7, 8, 9, 10 и 11.

Для решения задачи находим точки взаимного пересечения горизонталей обеих поверхностей, имеющих одинаковые отметки. Линия, соединяющая найденные точки, является искомой.

При по­строении линии пересечения топографической поверхности с конической поверхностью общего вида точки линии пересечения опре­деляются

как точки пересечения отдельных образующих кониче­ской поверхности с топографической поверхностью, по аналогии с рис. 30.

Рис. 32 Рис. 33

1.7.3. Пересечение топографической поверхности с цилиндрической поверхностью

Пусть на рис. 33 заданы топографическая поверхность и цилиндрическая поверхность с направляющей кривой M_l0N₁₃ и горизонтальными образующими. Соединяя точки взаимного пересечения горизонталей с одинаковыми отметками топографической и цилиндрической поверхностей, получаем проекции линии пересечения этих поверхностей.

Как указывалось выше, цилиндрическая поверхность с горизонтальными образующими может быть использована при решении задач на определение точки пересечения кривой линии с топогра­фической поверхностью. На данном чертеже точка К является точкой пересечения кривой M₁₀N₁₃ с заданной топографической поверхностью.

При пересечении топографической поверхности с цилиндри­ческой поверхностью с наклонными образующими задача сводится, как и при пересечении с конической поверхностью общего вида, к определению точек пересечения отдельных образующих цилинд­рической поверхности с топографической поверхностью.