1.3. Прямая и плоскость

1.3.1. Прямая в плоскости

В плоскости можно провести прямую с различным уклоном, но не превышающим уклон плоскости. Это означает, что интервал любой прямой, лежащей в плоскости, всегда больше интервала ма­сштаба уклона плоскости или равен ему.

Рассмотрим наиболее часто встречающиеся в практике случаи, когда требуется в заданной плоскости провести прямую заданного уклона и, наоборот, через данную прямую провести плоскость с заданным уклоном.

Пусть через точку А, лежащую на горизонтали плоскости Р (рис. 13), требуется провести прямую с заданным уклоном.

Для этого из точки а как из центра проведем окружность с радиусом R, равным интервалу прямой заданного уклона. В пересечении ее с соседней горизонталью отметим точки тип или т₁ и п₁. Прямые AM и AN лежат в плоскости Р и имеют заданный уклон.

На рис. 14 решена обратная задача: через прямую 5—8 про­ведены плоскости Р и Q с заданным уклоном (задача имеет два решения).

Так как горизонтали плоскости с целочисленными отметками должны проходить через точки прямой, имеющие такие же отметки, и проекции этих горизонталей должны быть расположены на расстояниях, равных интервалу масштаба уклона плоскости, то для решения задачи необходимо выполнить следующие построения. Из точки, лежащей на прямой и имеющей целочисленную отметку, например из точки 5 как из центра опишем дугу окружности с ради­усом R, равным заданному интервалу масштаба уклона плоскости. Из соседней точки прямой, например точки с отметкой 6, проведем касательные к окружности, которые будут являться горизонталями двух искомых плоскостей Р и Q.

Рис. 13 Рис. 14 Рис. 15

1.3.2. Прямая, пересекающая плоскость

Чтобы определить точку пересечения прямой 3—6 (рис. 15) с плоскостью Р, следует через данную прямую провести вспомога­тельную плоскость. Вспомогательную плоскость проводим с таким расчетом, чтобы проекции ее горизонталей с отметками 3 и 6 пере­секались с горизонталями таких же отметок плоскости Р в пределах чертежа.

Найдя точки а и b — точки взаимного пересечения горизонталей вспомогательной и заданной плоскостей и соединив их прямой линией, получим проекцию ab линии пересечения указанных плоско­стей. Точка п, полученная в пересечении прямой ab с проекцией прямой 3—6, является проекцией искомой точки пересечения задан­ной прямой с плоскостью Р.

Считая плоскость Р непрозрачной, получим, что невидимой части отрезка прямой будет соответствовать отрезок от точки п до точки 3, который и показан на чертеже штриховой линией.

1.3.3. Некоторые примеры на пересечение плоскостей

1. На горизонтальной плоскости с отметкой 10 требуется устроить земляную насыпь с площадкой ABCD заданной формы (рис. 16), расположенной на отметке 13. При заданных углах наклона откосов насыпи необходимо определить линии взаимного пересечения откосов, а также линии их пе­ресечения с плоскостью основания насыпи.

Для решения задачи строим вначале масштабы уклонов всех четырех откосов. Каждый масштаб будет перпендикулярен к соот­ветствующей стороне контура площадки ABCD, так как каждая сторона контура площадки представляет собой одновременно и горизонталь того или иного откоса насыпи. Затем с учетом масштаба чертежа проводим проекции других горизонталей откосов с интервалами, соответственно равными

и

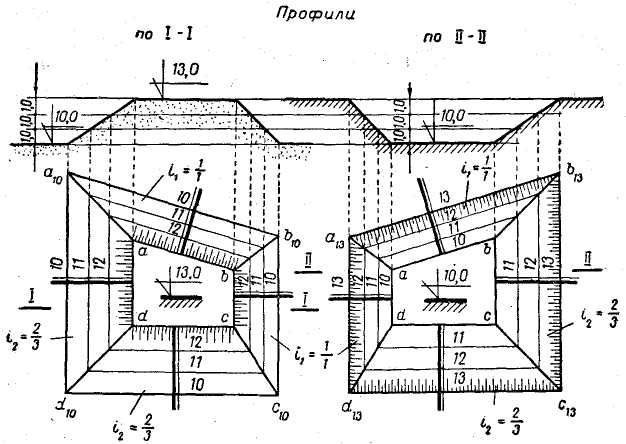
Рис. 16 Рис. 17

Линия пересечения смежных откосов насыпи будет проходить через точки пересечения горизонталей одинакового уровня. В тех случаях, когда откосы имеют одинаковые уклоны, а следовательно, и равные интервалы, проекция линии пересечения откосов может быть определена как биссектриса угла, образованного горизонта­лями этих откосов. Например, на чертеже линия dd10 идет по биссектрисе угла adc, а линия bb₁₀ — по биссектрисе угла abc.

Линиями пересечения от­косов насыпи с горизонталь­ной плоскостью ее основания являются горизонтали отко­сов с отметкой 10.

2. На рис. 17 приведен пример определения линий взаимного пересечения откосов выемки и линий пере­сечения откосов с горизонтальной плоскостью на от­метке 13,0, при устройстве площадки ABCD заданной формы — на отметке 10. Ук­лоны откосов выемки i₁ и i₂ приведены на чертеже. Как видно из чертежа, задача решается аналогично предыдущему примеру.

Следует указать, что при устройстве насыпей отметки горизон­талей откосов убывают, а при устройстве выемок возрастают в направлении от края площадки.

На чертежах откосы насыпей и выемок обозначаются так назы­ваемыми бергштрихами.

Бергштрихи проводятся по верхней кромке откоса перпендику­лярно к его горизонталям и в сторону горизонтали с меньшей от­меткой.

Рис. 18

3.На рис. 18 дана наклонная площадка ABCD (так называемая аппарель) с отметками точек А и В, рав­ными 10 м, и отметками точек С и D, равными 7 м. Уклон откосов выемки

Для определения линии пересечения откосов друг с другом и с горизонтальной плоскостью Н₁₀ необходимо провести горизонтали откосов выемки. Так как площадка ABCD является наклонной, то следует предварительно проградуировать ее, т.е. провести промежуточные горизонтали с отметками 8 и 9. Линия CD контура площадки — горизонтальная, поэтому масштаб уклонов торцевого откоса будет перпендикулярен к прямой cd, а горизонтали откоса будут параллельны ей.

Горизонталь откоса с отметкой 10 будет являться и линией пересечения откоса с плоскостью Н₁₀.

Для проведения горизонталей боковых откосов из точек а₈ и b₈ как из центров описываем дуги окружностей с радиусами, равными интервалу масштаба уклонов. Затем из точек a₉ и b₉ проводим каса­тельные к данным окружностям. Эти касательные представляют собой проекции горизонталей боковых откосов выемки с отметкой 9. Проекции остальных горизонталей боковых откосов будут соответ­ственно им параллельны.

Горизонтали боковых откосов и горизонтали торцевого откоса, имеющие одинаковые отметки, пересекаясь, определяют точки, при­надлежащие линии пересечения этих откосов. Так как уклоны всех откосов в данном случае одинаковы, то проекция линии взаимного пересечения откосов пойдет по биссектрисе угла а, составленного проекциями горизонталей бокового и торцевого откосов.

Горизонтали откосов, проведенные через точки а и b, определяют линию пересечения боковых откосов с горизонтальной плоскостью H_10.