МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО – ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ»

В Г.ЧИСТОПОЛЕ

ЛЕКЦИИ

по дисциплине:

«Инженерная графика»

(Проекции с числовыми отметками)

для специальности 270800.62

г. Чистополь

1. ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ

Метод проекций с числовыми отметками находит широкое применение при изображении земной (топографической) поверхности и при проектировании различных земляных сооружений.

1. 1. ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ ЛИНИИ

1.1.1. Проекции точки

В методе проекций с числовыми отметками применяется ортогональное проектирование на одну горизонтальную плоскость проекций Н₀, называемую обычно плоскостью нулевого уровня (р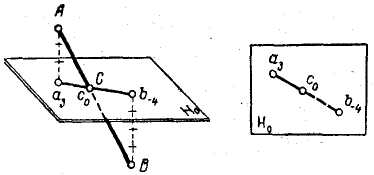ис. 1).

Рис. 1

Чтобы по проекциям точек судить о положении этих точек в пространстве, рядом с проекцией каждой точки проставляется циф­ра - отметка, указываю­щая расстояние в метрах от точки до плоскости нулевого уровня. Точки, расположенные над плоскостью нулевого уровня, имеют положительные отметки (точка А), а точки, расположенные ниже плоскости Н_о, — отри­цательные отметки (точка В). Точки, лежащие в плоскости уровня, имеют нулевую отметку (точка С).

Следует иметь в виду, что проекции точек могут не иметь буквенных обозначений. В этом случае рядом с проекциями точек проставляются только их отметки.

1.1.2. Проекции прямой

Прямая линия может быть задана проекциями двух любых ее точек. Например, прямая, соединяющая проекции а₃ и b_{- 4} точек A и В (рис. 1), является проекцией отрезка АВ прямой линии.

Проекция a₃b_₄ с учетом масштаба чертежа вполне определяет положение отрезка прямой в пространстве.*

(*На рис. 1 и на других чертежах, где рассматриваются теоретические основы проекций с числовыми отметками, масштабы как не имеющие в данном случае значения не приводятся).

Уклон и интервал прямой

Уклон прямой определяется тангенсом угла наклона прямой к плоскости уровня и обозначается i. Так, уклон прямой АВ (рис. 2) равен tg а, где

Из этого следует, что уклон прямой равен отношению алгебраической разности отметок концов отрезка к длине его проекции.

Длина проекции ab в методе проекций с числовыми отметками называется заложением отрезка прямой и обозначается буквой L.

Разность отметок концов отрезка прямой называется подъе­мом отрезка и обозначается буквой J.

Рис. 2 Рис. 3

Если разность отметок двух точек прямой равна единице, то заложение отрезка прямой, определяемого этими точками, назы­вается интервалом прямой и обозначается буквой l. Иными словами, интервалом прямой является заложение, соответ­ствующее подъему, равному единице.

Если точка С прямой АВ (рис. 2) выше точки А на 1м, то ас = l соответствует интервалу этой прямой. Как видно из чертежа, интервал l определяется из соотношения

Интервал и уклон прямой линии — величины, обратные друг другу, т.к. уклон прямой равен а интервал

На приведенном чертеже J = 4 и L = 6, следовательно, уклон прямой АВ равен

а интервал прямой АВ равен:

Из вышесказанного следует, что чем больше уклон прямой, тем меньше ее интервал и, наоборот, чем меньше уклон прямой, тем больше ее интервал. Например, уклон прямой АВ (рис. 3) боль­ше, чем уклон прямой СВ, а интервал l прямой АВ меньше интерва­ла l1 прямой СВ.

Градуирование прямой

Проградуировать прямую — это значит найти на ней точки, имеющие целочисленные отметки. Чтобы проградуировать прямую АВ, заданную проекцией a2,3 b6,4 (рис. 4), необходимо определить на проекции данной прямой положение проекций точек с отмет­ками 3; 4; 5 и 6. Для решения этой задачи может быть применен метод пропорциональ­ного деления.

Рис. 4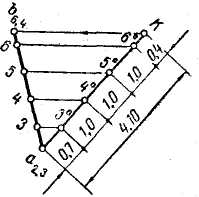 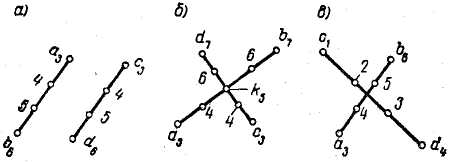Рис. 5

Проведем через точку а₂,з вспомогатель­ную прямую а2,3 К любого направления, от­ложим на ней от точки а₂,з отрезок, равный 0,7 единицы длины, например 0,7 см, и отметим точку 3°. Точки 4°, 5°,и 6° отстоят друг от друга на расстоянии 1 см, а точка К от точки 6° — на расстоянии, равном 0,4 см. Прямые, проведенные из точек 3°, 4°, 5° и 6° параллельно прямой Кb_6,4, определяют в пере­сечении с проекцией прямой искомые точки 3; 4; 5 и 6.

1.1.3. Относительное положение прямых

Если прямые взаимно параллельны (рис.5, а), то их проекции также взаимно параллельны, интервалы прямых равны друг другу и отметки точек прямых возрастают в одном и том же направлении.

Если прямые пересекаются (рис. 5, б), то их проекции также пересекаются, причем точка пересечения проекций представляет собой проекцию точки пересечения этих прямых.

Если проекции двух прямых не обладают свойствами, характерными для параллельных и пересекающихся прямых, то это озна­чает, что они являются проекциями скрещивающихся прямых (рис. 5, в).