
- •13. Задачі оптимізації використання взаємозамінних ресурсів
- •14. Оптимізація виробничої програми виробництва
- •15. Варіантні моделі виробничого планування
- •16. Задача оптимального вибору технологічних способів
- •17. Економічна інтерпретація двоїстих оцінок
- •18. Моделі оптимального розкрою промислових матеріалів
13. Задачі оптимізації використання взаємозамінних ресурсів
У задачах оптимального використання невзаємозамінних ресурсів у процесі виробництва виділялись ресурси якісно різних груп. У межах однієї групи ресурси вважають однорідними. Насправді ресурси зрідка бувають однорідними. Наприклад, кам’яне вугілля, видобуте з різних родовищ має відмінні характеристики. Так виникають задачі оптимального використання ресурсів у межах однієї групи, або задачі оптимального використання взаємозамінних ресурсів.
Для побудови економіко-математичної моделі задачі на максимум прибутку, за умови використання у виробничому процесі взаємозамінних ресурсів, введемо такі позначення:
i– індекс виду ресурсу в межах певної
групи,
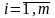 ;
;
j – індекс виду продукції,
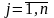 ;
;
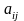 –
коефіцієнти затрат ресурсів і-го
виду, які використовують у виробництві
одиниці продукції j-го виду;
–
коефіцієнти затрат ресурсів і-го
виду, які використовують у виробництві
одиниці продукції j-го виду;
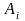 –
запас ресурсу і-го виду;
–
запас ресурсу і-го виду;
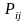 –
прибуток від реалізації одиниці продукції
j-го виду, яка вироблена з i-го
виду ресурсу;
–
прибуток від реалізації одиниці продукції
j-го виду, яка вироблена з i-го
виду ресурсу;
 –
кількість продукції j-го виду, яку
планують виробляти з i-го виду
ресурсу.
–
кількість продукції j-го виду, яку
планують виробляти з i-го виду
ресурсу.
Математична модель задачі є такою:
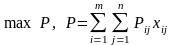 (1.8)
(1.8)
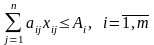 (1.9)
(1.9)
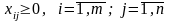 (1.10)
(1.10)
Функція мети (1.8) виражає сумарний прибуток від реалізації всієї продукції. Умова (1.9) показує обмеженість ресурсів кожного виду в межах певної групи. Умова (1.10) – умова невід’ємності обсягів виробництва продукції кожного виду.
Щоб побудувати економіко-математичну модель задачі на мінімум собівартості за умови використання у виробничому процесі взаємозамінних ресурсів, до вже введених позначень приєднаємо ще такі позначення:
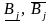 –
верхня і нижня межа виробництва продукції
j-го виду;
–
верхня і нижня межа виробництва продукції
j-го виду;
 –
собівартість виробництва одиниці
продукції j-го виду, виробленої з
i-го виду ресурсу.
–
собівартість виробництва одиниці
продукції j-го виду, виробленої з
i-го виду ресурсу.
Математична модель задачі є такою:
 (1.11)
(1.11)
(1.12)
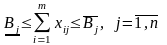 (1.13)
(1.13)
(1.14)
Функція мети (1.11) полягає в мінімізації сумарної собівартості випущеної продукції. Умова (1.12) показує обмеженість ресурсів кожного виду в межах певної групи. Умова (1.13) – умова виконання виробничої програми. Умова (1.14) – умова невід’ємності обсягів виробництва продукції кожного виду.
14. Оптимізація виробничої програми виробництва
З аналізу економіко-математичних моделей вибору оптимальної виробничої програми підприємства випливає висновок по те, що в розроблених моделях слід враховувати всілякі обмеження у різному поєднанні, а саме: контрольні завдання на випуск продукції; структуру обладнання; можливість поповнення обладнання; матеріальні ресурси; трудові ресурси; фонд заробітної плати; технологічні способи; структуру підприємства.
Усі ці фактори мають істотний вплив на формування річного плану підприємства, тому при побудові моделі будемо їх враховувати.
Обмеження на обсяг випуску продукції:
а) у натуральних одиницях:
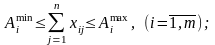 (2.1)
(2.1)
б) у вартісному виразі:
 (2.2)
(2.2)
де хij - шуканий обсяг
випуску виробів і –го виду j
-м виробничим способом;
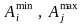 -
відповідно найменший і найбільший
рівень потреби в і –му виробі;
Pi- ціна виробу і –го
виду; P - товарний випуск продукції
у вартісному виразі.
-
відповідно найменший і найбільший
рівень потреби в і –му виробі;
Pi- ціна виробу і –го
виду; P - товарний випуск продукції
у вартісному виразі.
Обмеження по випуску продукції викликані тим, що підприємство як підсистема народного господарства повинно задовольняти народногосподарські потреби в даній продукції. Верхня межа Amax визначається попитом на даний вид продукції, а нижня межа Amin контрольним завданням її випуску.
Якщо організації, що випускають продукцію, задають підприємству загальний обсяг випуску продукції у вартісному виразі, то підприємство матиме більшу свободу вибору обсягових показників; заданий товарний випуск продукції виступає як нижня межа (це показано умовою (2.2).
Обмеження, визначені формулами (2.1) і (2.2) залежно від специфіки виробництва, можна записати разом або окремо. Або навіть їх можна віднести тільки до певних видів продукції.
Двостороннє обмеження (2.1) фактично виступає як дві нерівності:
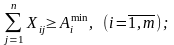

Для скорочення розмірності моделі і обсягу розрахункових операцій у таких випадках доцільно зробити заміну змінних за правилом

Це стає очевидним після проведення простих перетворень обмеження (2.1):

звідси
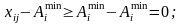

Якщо перейти до нових змінних
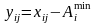
то другий з цих виразів матиме вигляд:
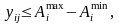
а перший є алгоритмічним обмеженням, тому додатково записувати його не треба.
У випадку такої заміни змінних необхідно провести відповідні перерахунки і в решті обмежень, і в цільовій функції.
Обмеження на фонд часу виробничого обладнання:
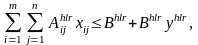 (2.4)
(2.4)

де
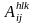 - норма витрат часу обладнання h -
ї групи, яке встановлене на l-й
дільниці k -го цеху, для проведення
робіт над i -м виробом на основі
j-го виробничого способу; Bhlk
- реальний річний фонд часу роботи
обладнання h-ї групи, встановленого
на l -й дільниці k - го цеху;
Bhlk - реальний річний фонд
часу роботи одиниці обладнання h
-ї групи, встановленого на l -й
дільниці k -го цеху; yhlk
- кількість одиниць додаткового
обладнання h -ї групи, яке повинно
бути встановлене на l - й дільниці
k -го цеху.
- норма витрат часу обладнання h -
ї групи, яке встановлене на l-й
дільниці k -го цеху, для проведення
робіт над i -м виробом на основі
j-го виробничого способу; Bhlk
- реальний річний фонд часу роботи
обладнання h-ї групи, встановленого
на l -й дільниці k - го цеху;
Bhlk - реальний річний фонд
часу роботи одиниці обладнання h
-ї групи, встановленого на l -й
дільниці k -го цеху; yhlk
- кількість одиниць додаткового
обладнання h -ї групи, яке повинно
бути встановлене на l - й дільниці
k -го цеху.
У випадку наявності нелімітованого обладнання для скорочення розмірності моделі його можна не брати до уваги. Правда, це пов”язано із значними витратами на перерахунки показників і може бути недоцільним.
Встановити додаткове обладнання можна при наявності вільної виробничої площі. Використання цієї площі можна задати наступним обмеженням.
Обмеження на виробничі площі:
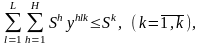 (2.5)
(2.5)
де Sh - норма площі на встановлення одиниці обладнання h -ї групи;
Sk - наявна вільна виробнича площа k -го цеху.
Обмеження на розмір капіталовкладень:
 (2.6)
(2.6)
де Ph - ціна одиниці обладнання h -ї групи; E - обсяг капіталовкладень, призначених для придбання нового обладнання.
Обмеження на трудові ресурси:
 (2.7)
(2.7)
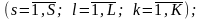
де
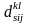 - норма витрати часу робітника s
-ї спеціальності l -ї дільниці k
-го цеху на обробку одиниці виробу i
-го виду j -м способом;
- норма витрати часу робітника s
-ї спеціальності l -ї дільниці k
-го цеху на обробку одиниці виробу i
-го виду j -м способом;
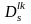 - реальний річний фонд часу роботи
робітників s -ї спеціальності l
-ї дільниці k-го цеху;
- реальний річний фонд часу роботи
робітників s -ї спеціальності l
-ї дільниці k-го цеху;
 -
річний реальний фонд часу роботи одного
робітника s -ї спеціальності
l -ї дільниці k -го цеху;
-
річний реальний фонд часу роботи одного
робітника s -ї спеціальності
l -ї дільниці k -го цеху;
 - додаткова кількість робітників s
-ї спеціальності l -ї дільниці
k -го цеху.
- додаткова кількість робітників s
-ї спеціальності l -ї дільниці
k -го цеху.
Обмеження на фонд заробітної плати:
 (2.8)
(2.8)
де rs - заробітна ставка
робітника s -ї спеціальності за
одиницю часу;
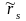 -
середня річна заробітна плата робітника
s -ї спеціальності; Ф - фонд
заробітної плати.
-
середня річна заробітна плата робітника
s -ї спеціальності; Ф - фонд
заробітної плати.
Обмеження на матеріали:
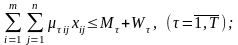 (2.9)
(2.9)
де
 - норма витрат матеріалу
- норма витрат матеріалу
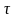 -го виду на одиницю виробу і -го
виду, який обробляють j -м способом;
-го виду на одиницю виробу і -го
виду, який обробляють j -м способом;
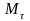 - ліміт матеріалу
-го виду;
- ліміт матеріалу
-го виду;
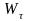 -шукане значення додатково закупленого
матеріалу
-го виду.
-шукане значення додатково закупленого
матеріалу
-го виду.
Обмеження на грошові ресурси, виділені на придбання матеріалу:
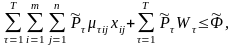 (2.10)
(2.10)
де
 - ціна одиниці матеріалу виду
;
- ціна одиниці матеріалу виду
;
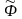 - фонд грошових ресурсів, що виділені
на придбання матеріалів.
- фонд грошових ресурсів, що виділені
на придбання матеріалів.
У випадку закупівлі всього лімітованого матеріалу, перший доданок в обмеженні (2.10) не беремо до уваги, а в грошових фондів значення зменшується на суму, сплачену за весь лімітований матеріал. Це обмеження набуває тоді вигляду:
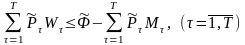 (2.11)
(2.11)
Визначаємо критерій оптимальності. Максимізація сумарного прибутку матиме вигляд:
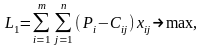 (2.12)
(2.12)
де Cij - повна собівартість виготовлення одиниці виробу i -го виду j -м виробничим способом.
Задача оптимізації річного плану підприємства може підпорядковуватись не тільки критерію (2.12). Іншими критеріями оптимальності для даної задачі можуть бути такі:
а) мінімізація сумарної собівартості продукції підприємства:
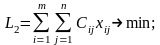 (2.13)
(2.13)
б) Мінімізація сумарної трудомісткості випуску продукції:
 (2.14)
(2.14)
в) Максимізація товарної продукції у вартісному виразі:
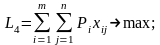 (2.15)
(2.15)
г) Максимізація рівня рентабельності:
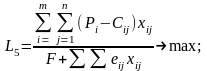 (2.16)
(2.16)
(тут F - вартість основних фондів; eij - норматив нормованих оборотних засобів на i -й виріб, виготовлений j -м виробничим способом).
