- •Примеры
- •Вывод из уравнений Ньютона
- •Физический смысл
- •Физический смысл работы
- •Определение
- •Работа силы (сил) над одной точкой
- •Работа силы (сил) над системой или неточечным телом
- •Кинетическая энергия
- •Потенциальная энергия
- •Консервативные силы
- •Диссипативные силы
- •Особенности
- •Пример диссипативных сил
- •Равномерное вращательное движение
- •Равнопеременное вращательное движение
- •Центр масс
- •Определение
- •Формулировка теоремы
- •Доказательство
- •Момент силы
- •Общие сведения
- •Единицы
- •Специальные случаи Формула момента рычага
- •Момент импульса в классической механике Определение
- •Вычисление момента
- •Сохранение углового момента
- •Момент инерции
- •Осевой момент инерции
- •Теорема Гюйгенса — Штейнера
- •Осевые моменты инерции некоторых тел
- •Энергия вращательного движения
- •Принцип относительности Галилея
- •Вид преобразований при коллинеарных осях
- •Релятивистская механика
- •Строгое определение
- •Релятивистское замедление времени
- •Второй закон Ньютона в релятивистской механике
Момент инерции
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,
,
где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
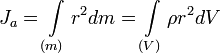 ,
,
где:
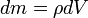 —
масса
малого элемента объёма тела
—
масса
малого элемента объёма тела 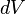 ,
,— плотность,
 —
расстояние
от элемента
до
оси a.
—
расстояние
от элемента
до
оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
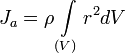
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
![]() ,
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
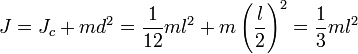
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения |
|
|||
Тело |
Описание |
Положение оси a |
Момент инерции Ja |
|
|
Материальная точка массы m |
На расстоянии r от точки, неподвижная |
|
|
|
Полый тонкостенный цилиндр или кольцо радиуса r и массы m |
Ось цилиндра |
|
|
|
Сплошной цилиндр или диск радиуса r и массы m |
Ось цилиндра |
|
|
|
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 |
Ось цилиндра |
|
|
|
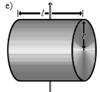
Сплошной цилиндр длины l, радиуса r и массы m |
Ось перпендикулярна к цилиндру и проходит через его центр масс |
|
|
|
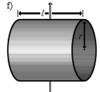
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m |
Ось перпендикулярна к цилиндру и проходит через его центр масс |
|
|
|
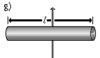
Прямой тонкий стержень длины l и массы m |
Ось перпендикулярна к стержню и проходит через его центр масс |
|
|
|
Прямой тонкий стержень длины l и массы m |
Ось перпендикулярна к стержню и проходит через его конец |
|
|
|
Тонкостенная сфера радиуса r и массы m |
Ось проходит через центр сферы |
|
|
|
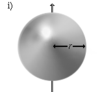
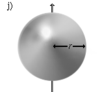
Шар радиуса r и массы m |
Ось проходит через центр шара |
|
|
|
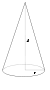
Конус радиуса r и массы m |
Ось конуса |
|
|
|
Равнобедренный треугольник с высотой h, основанием a и массой m |
Ось перпендикулярна плоскости треугольника и проходит через вершину |
|
|
|
Правильный треугольник со стороной a и массой m |
Ось перпендикулярна плоскости треугольника и проходит через центр масс |
|
|
|
Квадрат со стороной a и массой m |
Ось перпендикулярна плоскости квадрата и проходит через центр масс |
|
|