Формулировка теоремы
Нередко при рассмотрении движения системы полезно знать закон движения её центра масс. В общем случае этот закон, составляющий содержание утверждения теоремы о движении центра масс системы, формулируется следующим образом:
Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.
Доказательство
Пусть
система состоит из 
материальных
точек с массами 
и
радиус-векторами 
.
Как известно, центром масс (центром
инерции) системы материальных точек
называется геометрическая точка,
радиус-вектор 
которой
удовлетворяет равенству
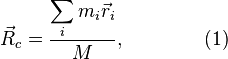
где
—
масса всей системы, равная 
Дифференцируя
(1) два раза по времени, для ускорения
центра масс 
получаем:
где 
—
ускорение материальной точки с номером i.
Для последующего рассмотрения целесообразно разделить все силы, действующие на тела системы, на два типа:
Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим .
Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать
.
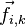Соответственно, сила воздействия i-й
точки на k-ю
точку будет обозначаться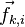 
.
Из
сказанного очевидно, что если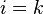 
,
то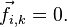 
Используя введённые обозначения, второй закон Ньютона для каждой из рассматриваемых материальных точек можно записать в виде
Суммируя все уравнения вида (3), получим:
Выражение 
представляет
собой сумму всех внутренних сил,
действующих в системе. Учтём теперь,
что по третьему закону Ньютона в этой
сумме каждой силе
соответствует
сила
такая,
что 
и,
значит, выполняется 
Поскольку
вся сумма состоит из таких пар, то и сама
сумма равна нулю. Таким
образом, из (4) следует
Далее,
обозначив 
и
подставив полученное выражение в (2),
приходим к уравнению
или
к 
Таким образом, движение центра масс определяется только внешними силами, а внутренние силы никакого влияния на это движение оказать не могут. Формула (6) является математическим выражением теоремы о движении центра масс системы.
Момент силы
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы.