- •Представление чисел Целые числа
- •Вычитание
- •Умножение
- •Деление
- •Беззнаковые целые
- •Простые типы данных
- •Тип данных char
- •Int a[10], b[20]; // 2 массива на 10 и 20 целых чисел
- •Int a[n]; // размер массива задан через константу
- •Int Sum ( int a[], int n ) // a[] – параметр-массив
- •Int a[20], b[30], s;// здесь надо ввести массивы a и b
- •Выражения
- •Операция присваивания
- •Арифметические операции
- •Операции сравнения
- •Порядок вычисления выражений
- •Выражения и операторы.
- •Цикл for
- •Цикл while
- •Цикл do-while
- •Оператор return
- •Оператор goto
- •Оператор break
- •Оператор continue
- •Очередь
- •Циклическая очередь в массиве
- •Рекуррентные соотношения
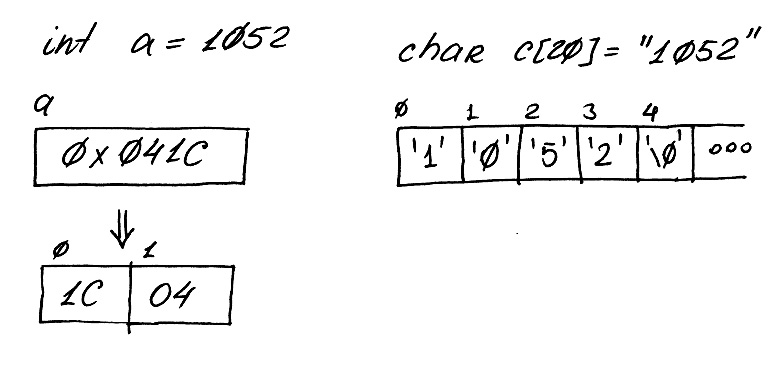
- •Внешняя и внутренняя форма представления числа
- •Классификация сортировок
- •Трудоемкость алгоритмов сортировки и поиска Сортировки выбором и вставками
- •Циклическое слияние группами по s элеметов
- •Исторический анализ
- •Логический анализ: cтандартные программные контексты
- •От общего к частному
- •Одно из трех
- •Особенности функции как модуля
- •Интерфейс передачи параметров в функцию
- •Примеры модульного проектирования
- •Сущность трансляции. Компиляция и интерпретация
- •Трансляция и ее фазы
- •Модульное программирование, компоновка
- •Понятие связывания. Статическое и динамическое связывание
- •Модульное проектирование на «классическом» Си Препроцессор
- •Области видимости и время жизни переменных
- •Все эти библиотеки условно разделены по категориям: Стандартные заголовочные файлы языка Си:
Рекуррентные соотношения
Рекуррентные соотношения определяют некоторый элемент последовательности через несколько предыдущих. Например, числа Фибоначчи: F(n)=F(n-1)+F(n-2), где F(0)=1, F(1)=1. Если рассматривать этот ряд от младших членов к старшим, способ его построения задается итерационным циклическим алгоритмом.
//-------------------------------------------------------------------------------------------------------
// Вычисление чисел Фибоначчи итерационным методом
// F2 – «позавчерашнее» значение ряда
// F1 – «вчерашнее» значение ряда
// F0 – «сегодняшнее» значение ряда
int FIBO(int n){
int F2=1,F1=1,n=1;
for (int i=0;i<n;i++) {
F0=F1+F2;
F2=F1,F1=F0; // при переходе к следующему шагу текущий становится
} // предыдущим
}
Программа для нахождения корня:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#include <math.h> #include <windows.h> #include <stdio.h>
double qvadr(double a, double b, double c); double qvadr(double a, double b, double c){ double d,x1,x2; d=b*b-4*a*c; if (d>0) {x1=(-b+sqrt(d))/(2*a);printf("%f",x1); x2=(-b-sqrt(d))/(2*a);printf("%f",x2); } if (d=0) {x1=(-b+sqrt(d))/(2*a);printf("%f",x1); } if (d<0) printf("net kornei"); return x1; } int main() { float a,b,c; scanf("%f%f%f",&a,&b,&c); printf("\n=%f\n",qvadr(a,b,c)); system("PAUSE"); return 0; } |
Программа для суммы ряда:
#include <iostream> #include <stdio.h> #include <math.h> #include <clocale> using namespace std; int fact(int k); double E; int k = 0; float Summ = 1, x, F; void main() { setlocale(0, "Rus"); cout << "Введите x" << endl; do { cin >> x; if (x == 0) cout << "Ошибка: x = 0, Введите данные заново!" << endl; } while (x == 0); cout << "Введите Е" << endl; do { cin >> E; if ((E < 0) || (E >= 1)) cout << "Ошибка, Введите данные заново!" << endl; } while ((E < 0) || (E >= 1)); double f = 1; while (true) { f *= -x * x * (2 * k + 1) / (2 * k * k + 5 * k + 1); // по признаку Даламбера рассчитан коэффициент на который отличаются следующий член ряда от предыдущего if (fabs(double (f)) < E) break; else Summ += f; // если точность больше чем член ряда, то выход из цикла, иначе накапливаем сумму cout << "Локальная сумма: " << f << endl; k++; } cout << "Конечная сумма: " << Summ << " полученная за " << k << " шагов." << endl; system("pause"); };
Строка. Строкой называется последовательность символов, ограниченная символом с кодом 0, то есть '\0'. Из ее определения видно, что она является объектом переменной размерности. Местом хранения строки является массив символов. Суть взаимоотношений между строкой и массивом символов состоит в том, что строка является структурой данных, а массив – переменной:
строка хранится в массиве символов, массив символов может быть инициализирован строкой, а может быть заполнен программно:
char A[20] = { 'С','т','р','о','к','а','\0' };
char B[80];
for (int i=0; i<20; i++) B[i] = 'A';
B[20] = '\0';
строка представляет собой последовательность, ограниченную символом '\0', поэтому работать с ней нужно в цикле, ограниченном не размерностью массива, а условием обнаружения символа конца строки:
for (i=0; B[i] !='\0'; i++)...
соответствие размерности массива и длины строки транслятором не контролируется, за это несет ответственность программа (программист, ее написавший):
char C[20],B[]=”Строка слишком длинная для C”;
// следить за переполнением массива
// и ограничить строку его размерностью
for (i=0; i<19 && B[i]!='\0'; i++) C[i] = B[i];
C[i]='\0';
Строковая константа - последовательность символов, заключенная в двойные кавычки. Допустимо использование неотображаемых символов. Строковая константа автоматически дополняется символом '\0', ею можно инициализироваться массив, в том числе такой, размерность которого определяется размерностью строки:
char A[80] = "123456\r\n";
char B[] = "aaaaa\033bbbb";
..."Это строка"...
Представление текста. Текст является последовательностью строк, и наш уровень работы с данными не позволяет предложить для его хранения что-либо иное, кроме массива двумерного массива символов:
char A[20][80];
char B[][40] = { "Строка","Еще строка","0000","abcdef"};
Первый индекс двумерного массива соответствует номеру строки, второй - номеру символа в нем:
for (int i=0; i<20; i++)
for (int k=0; A[i][k] !='\0'; k++) {…} // Работа c символами i-й строки
Внутренняя форма представления числа - представление числа в виде целой или вещественной переменной.
Внешняя форма представления числа - представление числа в виде строки символов – цифр в заданной системе счисления.
Функции и объекты стандартных потоков ввода/вывода могут, в частности, вводить и выводить целые числа, представленные в десятичной, восьмеричной и шестнадцатеричной системах счисления. При этом происходят преобразования, связанные с переходом от внешней формы представления к внутренней и наоборот.