Очередь
Объяснять, что такое очередь как способ организации данных, излишне, потому что здесь полностью применим житейский смысл этого понятия.
Очередь - последовательность элементов, включение в которую производится с одного, а исключение - с другого конца
Для способа хранения данных в очереди имеется общепринятый термин - FIFO (first in -first out - первый пришел, первый ушел).
Простейший способ представление очереди последовательностью, размещенной от начала массива, не совсем удобен, поскольку при извлечении из очереди первого элемента все последующие придется постоянно передвигать к началу.
//------------------------------------------------------61-01.cpp
// Очередь в массиве (от начала, со сдвигом)
void in(int vv){ if (n!=SZ-1) A[n++]=vv;}
int out(){
if (n==0) return 0;
int vv=A[0];
for (int i=0;i<n-1;i++) A[i]=A[i+1];
n--;
return vv;
}
int get(int k){ return k>=n ? 0 : A[k]; }
Альтернативный вариант - у очереди должно быть два указателя - на ее начало в массиве и на ее конец (точнее, индекс первого элемента и индекс следующего за последним, т.е. первого свободного). По мере постановки и извлечения из очередт оба они будут продвигаться к концу массива. Выход из создавшегося положения – «зациклить» очередь, то есть считать, что за последним элементом массива следует опять первый. Подобный способ организации очереди в массиве называют циклическим буфером.
Циклическая очередь в массиве
//------------------------------------------------------61-01.cpp
// Циклическая очередь в массиве
int fst=0,lst=0;
void in(int vv){
if ((lst+1)%SZ==fst) return;
A[lst++]=vv;
if (lst==SZ) lst=0;
}
int out(){
if (fst==lst) return 0;
int vv=A[fst++];
if (fst==SZ) fst=0;
return vv;
}
int get(int m){ return A[(fst+m)%SZ]; }
В отличие от стека указатель на конец очереди (lst) ссылается не на последний занятый, а на первый свободный элемент массива. Условие fst==lst означает, что очередь пуста, а выражение (lst+1)%SZ==fst – что очередь заполнена (при перемещений индекс конца очереди попадает на начало).
Цикл -- разновидность управляющей конструкции в высокоуровневых языках программирования, предназначенная для организации многократного исполнения набора инструкций. Также циклом может называться любая многократно исполняемая последовательность инструкций, организованная любым способом (например, с помощью условного перехода).
Исполнение любого цикла включает первоначальную инициализацию переменных цикла, проверку условия выхода, исполнение тела цикла и обновление переменной цикла на каждой итерации. Кроме того, большинство языков программирования предоставляют средства для досрочного управления циклом, например, операторы завершения цикла, то есть выхода из цикла независимо от истинности условия выхода.
Итерационные циклы – это циклы, в которых число повторений циклов заранее не известно и зависит от некоторых условий.
Пример. Вычислить 
при k=1,
2, … .
Определить k при
котором y становится
больше a.
Решение: Схема алгоритма имеет вид
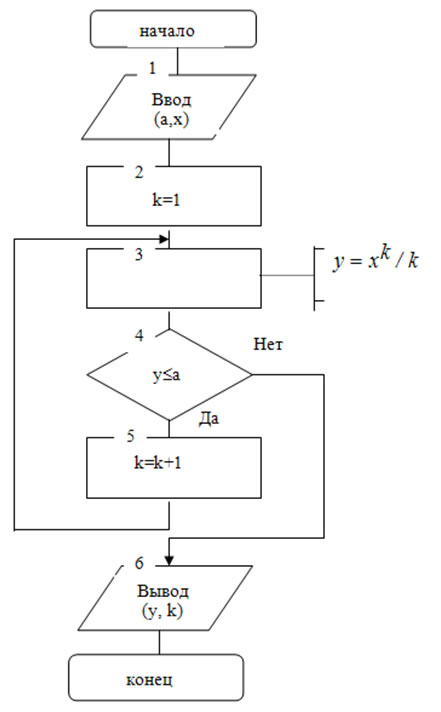
Алгоритм итерационного цикла
Рекурсивным называется способ построения объекта (понятия, системы, описание действия), в котором определение объекта включает аналогичные объекты (понятие, систему, действие) в виде составных частей.
Линейная рекурсия. Простейшим примером рекурсии является линейная рекурсия, когда функция содержит единственный условный вызов самой себя. В таком случае рекурсия становится эквивалентной обычному циклу. Действительно, любой циклический алгоритм можно преобразовать в линейно-рекурсивный и наоборот.
//-------------------------------------------------------------------------------------------------------
//----- Циклический алгоритм вычисления факториала
int fact(int n) {
for (int s=1; n!=0; n--) s *=n;
return s;}
//------ Рекурсивный алгоритм вычисления факториала
int fact(int n) {
if (n==1) return 1;
return n * fact(n-1); }
Рекурсивная функция и стек. Каждый рекурсивный вызов порождает новый «экземпляр» формальных параметров и локальных переменных, причем старый «экземпляр» не уничтожается, а сохраняется в стеке по принципу вложенности. Здесь имеет место единственный случай, когда одному имени переменной в процессе работы программы соответствуют несколько ее экземпляров. Происходит это в такой последовательности:
- в стеке резервируется место для формальных параметров, в которые записываются значения фактических параметров. Обычно это производится в порядке, обратном их следованию в списке;
- при вызове функции в стек записывается точка возврата - адрес той части программы, где находится вызов функции;
- в начале тела функции в стеке резервируется место для локальных (автоматических) переменных.
Перечисленные переменные образуют группу (фрейм стека). Стек «помнит историю» рекурсивных вызовов в виде последовательности (цепочки) таких фреймов. Программа в каждый конкретный момент работает с последним вызовом и с последним фреймом. При завершении рекурсии программа возвращается к предыдущей версии рекурсивной функции и к предыдущему фрейму в стеке.