1. Позиционная система счисления — система, в которой значение символа зависит от его места в ряду цифр, изображающих число. Например, в числе 7382 первая цифра слева означает количество тысяч, вторая — количество сотен, третья — количество десятков и четвёртая количество единиц. Позиционные системы счисления (ПСС) более удобны для вычислительных операций, поэтому они получили более широкое распространение. Позиционная система счисления характеризуется основанием.

Двоичная система счисления. Правила двоичной арифметики

В двоичной системе счисления для записи чисел используется две цифры 0 и 1. Основание системы q=2 записывается как 10₂=[1*2¹+0*2⁰]₁₀

В данной СС любое число может быть представлено последовательностью двоичных цифр. Эта запись соответствует сумме степеней цифры 2, взятых с указанными в ней коэффициентами

X=am*2m+am-1*2m-1+…+a1*21+a0*20+… . Например, двоичное число (10101101)2=1*27+0*26+1*25+0*24+1*23+1*22+0*21+1*20=17310

Арифметические операции над двоичными числами отличаются простотой и лег-костью технического выполнения.

Правила двоичной арифметики:

Сложение:

0+0=0;

1+0=1;

0+1=1;

1+1=10 (происходит перенос единицы в старший разряд);

Вычитание:

0-0=0;

1-1=0;

1-0=1;

10-1=1 (происходит заем единицы в старшем разряде);

Умножение:

0х0=0;

1х0=0;

0х1=0;

1х1=1;

Двоичная система счисления является основной для использования в ЭВМ, удобной из-за простоты выполнения арифметических операций над двоичными числами. С точки зрения затрат оборудования на создание ЭВМ эта система уступает только троичной системе счисления.

В двоично-кодированных системах счисления, имеющих основания q, отличные от 2 (q>2), каждая цифра числа представляется в двоичной системе счисления. Наибольшее применение в ЭВМ получили шестнадцатеричная система счисления и десятичная двоично-кодированная система счисления.

Перевод целых чисел

Допустим, число Х из системы счисления с основанием q требуется перевести в систему счисления с основанием р. Перевод осуществляется по следующему правилу. Целую часть числа делим на новое основание р. Полученный от деления первый остаток является младшей цифрой целой части числа с основанием р. Целую часть полученного числа снова делим на основание р. В результате определим второй остаток, равный следующей после младшей цифре числа с основанием р', деление будем производить до тех пор, пока не получим частное меньше делителя. Последнее частное дает старшую цифру числа с основанием р.

Пример

Число 26₁₀ перевести в двоичную систему счисления. Перевод осуществим методом последовательного деления десятичного числа 26 на основание новой системы счисления - 2. Остатки от деления образуют искомое число в двоичной СС. Таким образом:

В результате получаем 26₁₀ = 11010₂

Пример

Число 191₁₀ перевести в восьмеричную систему счисления. Перевод осуществим методом последовательного деления десятичного числа 191 на основание новой системы счисления - 8. Остатки от деления образуют искомое число в восьмеричной СС.Остатки отделения образуют восьмеричное число

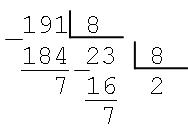
В результате получаем 191₁₀ = 277₂

Перевод из позиционной СС в десятичную:

Перевод из любой позиционной системы счисления в десятичную осуществляется следующим методом:

1) над каждым разрядом числа расставляют его номер по порядку справа налево, начиная с нуля; 2) цифры числа являются коэффициентами при основании системы счисления в степенях соответствующих номеру разряда; 3) суммируют полученные произведения оснований системы счисления в степенях равных соответствующему номеру разрядов на цифры числа.

Рассмотрим данный алгоритм на примере перевода 1101001₂ в десятичную СС: 1101001₂ = [1*2⁶+1*2⁵+0*2⁴+1*2³+0*2²+0*2¹+1*2⁰]₁₀ = 105₁₀

Представление чисел Целые числа

Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.  Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.  Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.  В любом представлении старший бит определяет знак числа:  0 - положительное число;  1 - отрицательное число

ПРИМЕР.

Для числа +1101:

Прямой код	Обратный код	Дополнительный код
0,0001101	0,0001101	0,0001101

Для числа -1101:

Прямой код	Обратный код	Дополнительный код
1,0001101	1,1110010	1,1110011

В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).

Сложение

Сложение одноразрядных двоичных чисел выполняется по следующим правилам:

0 + 0 = 0

1 + 0 = 1

0 + 1 = 1

1 + 1 = 10

Сложим для примера два любых двоичных числа:

1101

+ 101

------

10010

Вычитание

Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:

0 - 0 = 0

1 - 0 = 1

0 - 1 = (заем из старшего разряда) 1

1 - 1 = 0

Пример:

1110

- 101

----

1001

Умножение

Умножение одноразрядных двоичных чисел выполняется по следующим правилам:

0 * 0 = 0

1 * 0 = 0

0 * 1 = 0

1 * 1 = 1

Пример:

1110

* 10

------

+ 0000

1110

------

11100

Деление

Деление выполняется так же как в десятичной системе счисления:

1110 | 10

|----

10 | 111

----

11

10

----

10

10

----

0

2. Основные структурные единицы памяти компьютера: бит, байт, машинное слово.  Бит. Все данные и программы, хранящиеся в памяти компьютера имеют вид двоичного кода, один символ, которого несет 1бит информации. Ячейка памяти, хранящая один двоичный знак, называется «бит». В одном бите памяти храниться 1 бит информации. Битовая структура памяти определяет свойство памяти дискретность  Байт. Восемь расположенных подряд битов памяти образуют байт. В одном байте памяти хранится один байт информации. Во внутренней памяти все байты пронумерованы. Нумерация начинается с нуля. Порядковый номер байта называется его адресом. В ПК адреса обозначаются двоичным кодом. Используется также 16-ричная форма обозначения адреса. Машинное слово.  Наибольшая последовательность бит, которую процессор может обрабатывать как единое целое, наз. машинным словом Длина машинного слова может быть 8, 16, 32, 64 бита и т.д.; адрес машинного слова равен адресу младшего байта, входящего в это слово Занесение информации в память, а также извлечение ее из памяти производится по адресам. Это свойство называется адресуемостью.

1Кбайт = 1024 байта

1Мбайт=1024 кбайта= 1 048 575байт

1Гбайт = 1024 Мбайт=1 048 575 Кбайт= 1 073 740 800 байт

Пример 1 Компьютер имеет ОЗУ 2 Кбайта. Указать адрес последнего байта оперативной памяти(десятичный, двоичный, 16-ричный. Решение. Объем ОЗУ =2048 байт. Адрес последнего байта – 2047, т.к. нумерация начинается с 0. 204710 = 7FF16 = 0111 1111 11112

Пример2. Объем ОЗУ равен 1 Мбайту, а адрес последнего машинного слова – 1048574. Чему равен размер маш.слова? Решение: 1Мбайт= 1024 Кбайта= 1 048 576 байт. Т.к. нумерация байтов начинается с 0, то адрес последнего байта =1 048 575. Таким образом, последнее машинное слово включает в себя 2 байта с номерами 1 048 574 и 1 048 575. Ответ: 2 байта

 Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния  «выключено» и «включено», либо «нет» и «да». Состоянию «выключено» или «нет» соответствует цифра 0, а состоянию «включено» или «да» цифра 1. Простым пользователям обычно нет необходимости полностью понимать устройство компьютера, однако двоичная система счисления дает о себе знать в виде различных ограничений основанных на степени двойки. Более компактный вариант двоичной системы называют шестнадцатеричной. Число шестнадцать является четвертой степенью числа два. Из этого следует, что можно достаточно просто переводить длинных двоичные последовательностей из нулей и единиц в короткие шестнадцатеричные. Для этого достаточно разбить двоичную последовательность на группы по четыре разряда (цифры) начиная с младшего разряда (справа) и заменить каждую группу на соответствующее шестнадцатеричное значение.

Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2¹⁶), а двоичной 2. Двоичная последовательность может быть достаточно громоздкой. Например, запись числа 513 требует десять двоичных разрядов (1000000001), а в шестнадцатеричной только три (201). Тем не менее, для представления любых шестнадцатеричных чисел требуется шестнадцать разных символов, а не десять, которые используются в привычной нам десятичной системе счисления. Первые десять символов это символы в интервале от 0 по 9, остальные это буквы латинского алфавита в интервале от A по F. Буквы обычно (но не всегда) пишут в верхнем регистре (заглавные) в шестнадцатеричной записи числа. Первые десять символов (от 0 по 9) записываются аналогично цифрам в десятичной системе счисления и соответствуют им. Буквы в интервале от A по F соответствуют значениям в интервале от 10 до 15.

Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.

ДЕСЯТИЧНАЯ ЗАПИСЬ	ШЕСТНАДЦАТЕРИЧНАЯ ЗАПИСЬ	ДВОИЧНАЯ ЗАПИСЬ
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Записи 10, 11 и т. д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.

Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10² + 2*10¹ + 3*10⁰. Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16³ + 10*16² + 5*16¹ + 14*16⁰ = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.

Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E  может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.

Т.к. каждый двоичный разряд может принимать два значения, два разряда – четыре и т.д., то для n-разрядного слова получим W=2ⁿ сочетаний (или возможных значений). Причем это не зависит от формы представления данных, будь то символы текста, цветовая палитра или диапазон целого числа. Например, кодовая таблица представления символов текстового файла в формате один символ – один байт содержит 2⁸=256 значений, 32-разрядное машинное слово представляет целое без знака в диапазоне 0… 232-1, т.е. 232 значений. Кстати «сколько это будет в граммах»? Точнее в десятичной системе.

Совсем необязательно для этого считать степени двойки. Информационная емкость трех десятичных цифр (разрядов) примерно соответствует аналогичной емкости десяти двоичных разрядов. Это можно использовать для оценки информационной емкости машинных слов. Например, для 32-разрядного слова W=2³²=2^2.2^10.2^10.2¹⁰ ≈ 4^.10^3.10^3.10³=4^.10⁹