12.Составление симплекс таблиц. Критерий оптимальности

Симплекс –метод основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает при условии, что задача имеет оптимальный план и каждый опорный план является невырожденным.

Этот переход возможен, если известен какой-либо опорный план.

В этом случае каноническая задача линейного программирования должна содержать единичную подматрицу порядка m

Тогда очевиден первоначальный опорный план( неотрицательное базисное решение системы ограничений КЗЛП).

План, при котором целевая функция ЗЛП принимает свое максимальное

(минимальное ) значение , называется оптимальным

Этот план определяется системой единичных векторов , которые образуют базис m-векторного пространства.

Проверка на оптимальность опорного плана происходит с помощью критерия оптимальности.

Критерий оптимальности (критерий оптимизации) — характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может быть установлено несколько критериев оптимальности.

13. Признак оптимальности опорного плана

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

, где  ,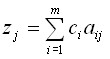 

то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения; если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

Теорема 2. Если для всех векторов выполняется условие  , то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор  , давший минимальную отрицательную величину симплекс-разности:  .

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор  г, который дает минимальное положительное отношение:

;  , .

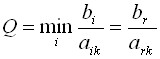14. Транспортная задача. Постановка задачи

Постановка задачи:

Однородный груз сосредоточен у m поставщиков в объемах а₁, а₂, …, а_m.

Данный груз необходимо доставить n потребителям в объемах, b₁, b₂, … , b_n.

Известен С_ij (i= 1, 2, … , m; j=1, 2 ,…, n) – стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю.

Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны. Исходные данные транспортной задачи записываются в таблице вида:

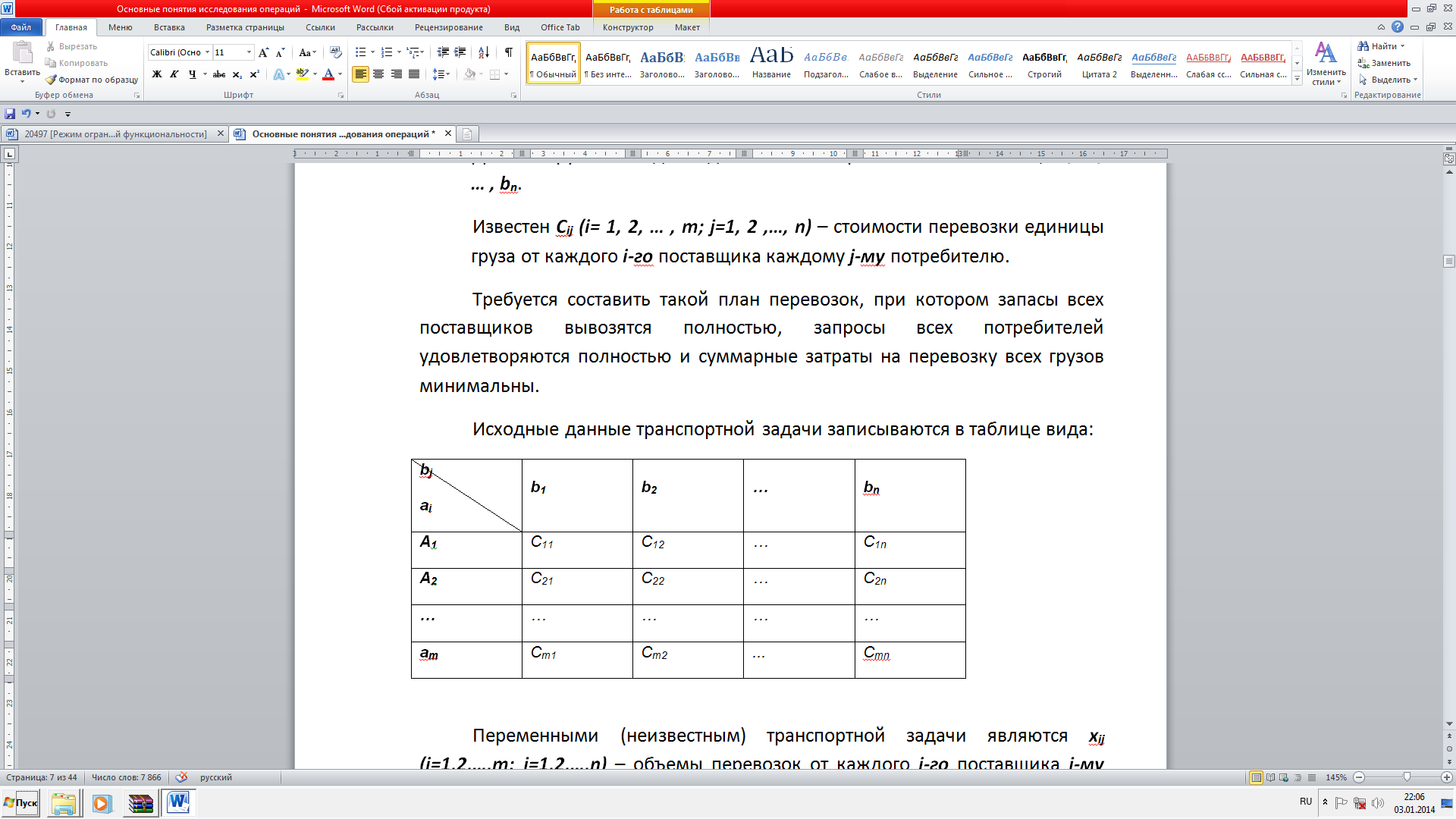
Переменными (неизвестным) транспортной задачи являются x_ij (i=1,2,…,m; j=1,2,…,n) – объемы перевозок от каждого i-го поставщика j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок.