9. Третья теорема двойственности:

Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи линейного программирования, т.е.

В последнем выражении дифференциалы заменим приращениями. Тогда получим выражение: , если , тогда , Экономическое содержание третьей теоремы двойственности: двойственная оценка численно равна изменению целевой функции при изменении соответствующего ресурса на единицу. Двойственные оценки y_j часто называются скрытыми теневыми или маргинальными оценками ресурсов.

10. Решения задачи линейного программирования графический методом. Алгоритм решения

ейного программирования применяется только в случае двух переменных. Стандартная задача линейного программирования для двух переменных имеет вид F = c₁x₁+c₂x₂ при ограничениях 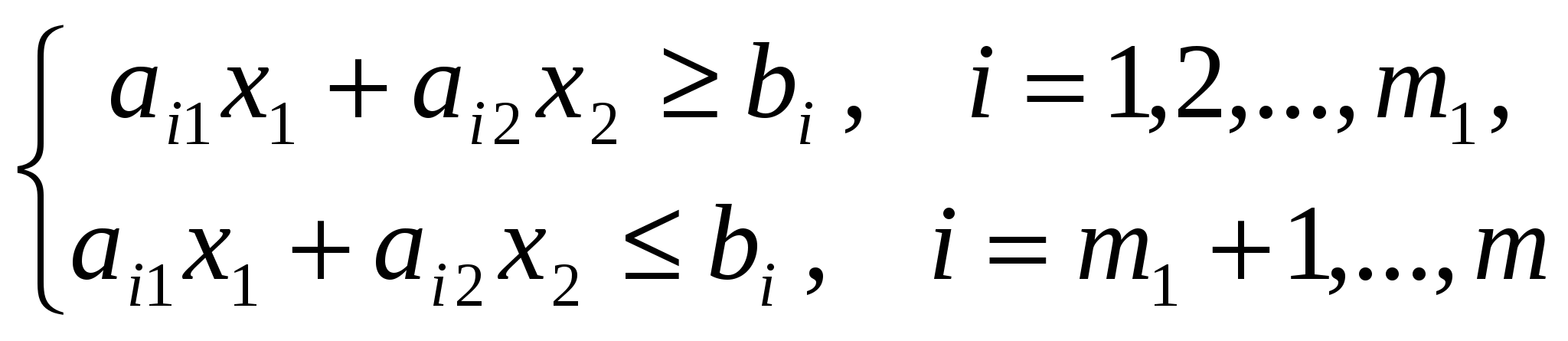. Пусть геометрическим изображением системы ограничений является выпуклый многоугольник ABCDEG (рис. 5.1). Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F = c₁x₁+c₂x₂ принимает максимальное (или минимальное) значение. При использовании графического метода используется линия уровня. Линией уровня функции F(x₁;x₂) называется множество всех точек (x₁;x₂), в которых функция принимает постоянное значение а, т.е. F =a, или c₁x₁+c₂x₂=а. (5.1) Итак, на многоугольнике решений следует найти точку, через которую проходит линия уровня функции F с наибольшим (если линейная функция максимизируется) или наименьшим (если она минимизируется) уровнем. Уравнение линии уровня функции (5.1) есть уравнение прямой линии. При различных значениях а линии уровня параллельны, так как их угловые коэффициенты определяются только соотношением между коэффициентами с₁ и с₂ и, следовательно, равны. Свойство линии уровня линейной функции. При параллельном смещении линии в одну сторону у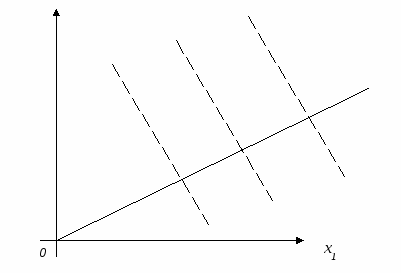 ровень только возрастает, а при смещении в другую сторону – только убывает. Пусть имеется три линии уровня F = c₁x₁+c₂x₂ = а₁, (І) F = c₁x₁+c₂x₂=а₂, (ІІ) F = c₁x₁+c₂x₂=а₃, (ІІІ) причем линия (ІІ) заключена между линиями (І) и (ІІІ). Тогда a₁<a_{2<a3</a</a или a1>a2>a3. В самом деле, на линии (перпендикулярной к линиям уровня (рис.5.2)) уровень является линейной функцией, а значит, при смещении в одном из направлений возрастает, а в другом убывает. х2 ІІІ ІІ І F=a3 F=a1 F=a2 Рис. 5.2 Таким образом, все линии уровня являются прямыми, перпендикулярными общему вектору нормали , определяемому соотношением , где и - орты осей х1 и х2 соответственно. Таким образом, координаты вектора являются коэффициентами целевой функции F(x1;x2). При увеличении а прямая F = a смещается параллельно самой себе в направлении вектора .}

_13. Если все числа для j=1,2,...,n.

11. Симплекс-метода решения задач линейного программирования

Симплексный метод – метод последовательного улучшения плана.

Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования. Математическая модель задачи приводится к каноническому (стандартному) виду. Заполняется опорная симплекс – таблица с использованием коэффициентов целевой функции и системы ограничений. Решается задача по алгоритму.

Идея симплексного метода заключается в том, что начиная с некоторого исходного опорного решения, осуществляется последовательно направленное перемещение по допустимым решениям к оптимальному. Значение целевой функции для задач на максимум не убывает. Так как число допустимых решений, конечно, то через конечное число шагов получим оптимальное решение.

Алгоритм симплексного метода

1.Математическую модель задачи привести к каноническому виду.

2.Построить начальную симплекс-таблицу исходя из стандартного вида.

3. Найти разрешающий столбец. В строке коэффициентов ЦФ найти значение с самим маленьким отрицательным числом. Этот столбец и будет разрешающим.

4. Вычислить разрешающую строку и ведущий элемент.

5.Построить новую симплекс-таблицу-второй шаг.

При построении новой таблицы убрать из базиса строку с переменной разрешающей строки в предыдущей таблице. Ввести в базис строку с названием разрешающего столбца предыдущей таблицы.

• Построение ведущей строки в новой таблице. По члена поделить всю разрешающую строку на разрешающий элемент.

• Построение других строк в новой таблице. По члена умножить ведущую строку на соответствующие этим строкам элементы разрешающего столбца из предыдущей таблицы и прибавить к соответствующим строкам в старой таблице.

6. Проверяем таблицу второго шага на оптимальность. Если в строке целевой функции нет отрицательных элементов, тогда таблица имеет оптимальный план, записать ответ. Если в строке ЦФ есть отрицательный элемент, тогда переходят к следующему шагу, строят новую симплекс-таблицу и затем проверяют ее на оптимальность. Построение таблиц заканчивается с нахождением оптимального плана.

Прямая задача на минимум решается следующим образом:

• Написать математическую модель двойственной задачи в стандартном виде

• Решить двойственную модель симплекс - методом

• Записать ответ.

Связь между задачами двойственной пары в том, что, решая симплексным методом одну из них, автоматически получаем решение другой.