5. Постановка задачи линейного программирования.

Общая постановка задачи

Линейное программирование — наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Определение.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как

Z(x)=C₁X₁+C₂X₂ + ^{. . .} +С_JX_J + ^{. . .} +С_nX_{n _} max(min)

при ограничениях:

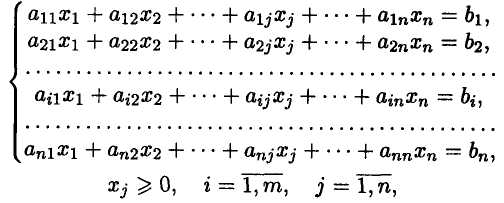
где X_i — неизвестные;a _ij , b_j , C_i — заданные постоянные вели­чины.

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.

М атематическая модель в более краткой записи имеет вид: Z(x) = ∑C_i X_i max(min)

при ограничениях:

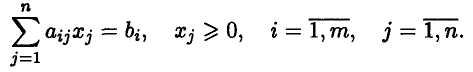
Определение Допустимым решением зада­чи линейного программирования называется вектор

X = (х₁, х₂, ,...х_n ) , удовлетворяющий системе ограничений.

Множество допустимых решений образует область допус­тимых решений (ОДР).

Определение Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается Х_опт.

Базисное допустимое решение

Является опорным решением, где r— ранг системы ограничений.

6. Формы представления злп.

   1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

(10.10)

при условиях

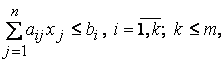(10.11)

(10.12)

                                              .                                 (10.13)

Функция  (10.10) называется целевой функцией (или линейной формой) задачи (10.10) – (10.13), а условия (10.11) – (10.13) – ограничениями данной задачи.

2. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального для «≤» (минимального для «≥») значения функции (10.10) при выполнении условий (10.11) и (10.13), где k = m, s = n.

3. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (10.10) при выполнении условий (10.12) и (10.13), где k = 0, s = n.

Каноническая (основная) форма	Стандартная (симметричная) форма	Общая форма
1) ограничения
Уравнения .	Неравенства .	Уравнения и неравенств .
2) условия неотрицательности
Все переменные ,	Все переменные ,	Часть переменных , , .
3) цель задачи
max F(x) или minF(x)	max F(x) [min F(x)]	max F(x) или min F(x)

Замечание.

max F(x) = – min[– F(x)], min F(x) = – max[– F(x)].

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них может быть преобразована к форме другой. Совокупность чисел , удовлетворяющих ограничениям (10.11) – (10.13), называется допустимым решением (или планом).

Запишем основную задачу линейного программирования в векторной форме. Найти максимум (минимум) функции

при условиях

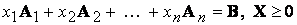                                  ,                   (10.14)

где  – скалярное произведение;  и  – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членов системы уравнений задачи.

План Х называется опорным планом основной задачи линейного программирования, если система векторов , входящих в разложение (10.14) с положительными коэффициентами , линейно независима.

Опорный  план  называется  невырожденным,  если  он  содержит ровно m положительных компонент, в противном случае он является вырожденным.

План , при котором целевая функция принимает свое максимальное (минимальное) значение, называется оптимальным.
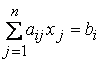