24. Множества, операции над множествами.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами   , а элементы множества строчными латинскими буквами   .

Запись   означает, что есть множество   с элементами  , которые связаны между собой какой-то функцией   .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

Принадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   принадлежит множеству   ).

Непринадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   не принадлежит множеству   ).

Объединение множеств:   .

Объединением двух множеств   и   называется множество   , которое состоит из элементов множеств   и   , т.е.

 или

Пересечение множеств:   .

Пересечением двух множеств   и   называется множество   , которое состоит из общих элементов множеств   и   , т.е.

   и

Разность множеств:   .

Разностью двух множеств   и   , например, множество   минус множество   , называется множество   , которое состоит из элементов множества   , которых нет в множестве   , т.е.

   и

Симметрическая разность множеств:   .

Симметрической разностью двух множеств   и   называется множество   , которое состоит из не общих элементов множеств   и   , т.е.

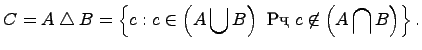
Дополнение множества:   .

Если предположим, что множество   является подмножеством некоторого универсального множества   , тогда определяется операция дополнения:

   и

Вхождение одного множества в другое множество:   .

Если любой элемент множества   является элементом множества   , то говорят, что множество   есть подмножество множества   (множество   входит в множество   ).

Не вхождение одного множества в другое множество:   .

Если существует элемент множества   , который не является элементом множества   , то говорят, что множество   не подмножество множества   (множество   не входит в множество   ).

25. Множество действительных чисел. Абсолютная величина действительного числа и ее свойства.

Объединение множества рациональных чисел и множества иррациональных чисел называется множеством действительных (или вещественных) чисел.  Множество действительных чисел обозначается символом R. 

бсолютной величиной (или модулем) действительного числа а называется неотрицательное действительное число, удовлетворяющее условиям:

Из определения следует, что а ≤ │а│ для любого а.

Свойства абсолютных величин.

1.           Абсолютная величина алгебраической суммы нескольких действительных чисел не больше суммы абсолютных величин слагаемых

.

2.           Абсолютная величина разности не меньше абсолютных величин уменьшаемого и вычитаемого

> .

3.           Абсолютная величина произведения равна произведению абсолютных величин

.

4.           Абсолютная величина частного равна частному абсолютных величин  делимого и делителя

.

26. Функция. Способы задания функции. График функции. Четные и нечетные функции, монотонные функции, периодические функции.

Опр. 1. Рассмотрим два множества Х и У, элементами которых могут быть любые объекты. Предложим, что каждому элементу х множества Х по некоторому закону f или способу поставлен в соответствие определенный элемент у множества У, тогда говорят что на множестве Х задана функция у = ƒ(х) (или отображение множества Х во множество У). Множество Х называется областью определения функции ƒ, а элементы у=ƒ(х) образуют множество значений функции – У, х – независимая переменная (аргумент), у – зависимая переменная, ƒ – закон соответствия, знак функции.

Способы задания функции. Существует несколько способов задания функции:

а) аналитический способ, если функция задана формулой вида у= f(х);

б) табличный способ состоит в том, что функция задается таблицей, содержащей значения х и соответствующие значения f(х);

в) графический способ, состоит в изображении графика функции – множество точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения функции у=f(х);

г) описательный способ, если функция записывается правилом ее составления.

Основные элементарные функции:

Степенная функция у=хα;

Показательная функция у=ах, а > 0, а ≠ 1;

Логарифмическая функция у=logах, а>0, а ≠ 1;

Тригонометрические функции: у=sinх, у=cosх , у=tgх, у=ctgх;

Обратные тригонометрические функции у=argsinх, у=arccosх, у=arctgх, у=arcctgх.

Под основными свойствами функции у=f(x) будем понимать следующие шесть:

1) область определения D(f);

2) область значений E(f);

3) четность, нечетность;

4) монотонность;

5) ограниченность;

6) периодичность.

Четность и нечетность.

Орп. 1. Функция у=f(x) называется четной, если для любых значений х из области определения f(-x)=f(x) и нечетной, если f(-x)=-f(x). В противном случае функция у=f(x) называется функцией общего вида.

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. Поэтому для четной функции достаточно строить лишь правую половину графика (х≥0); левая половина его (х≤0) является зеркальным отражением правой относительно оси Оу.

Чтобы построить график нечетной функции, достаточно изобразить правую половину его (х≥0); левая половина графика (х≤0) получается в результате поворота правой на 180°.

Монотонность.

Опр. 2. Функция у=f(x) называется строго возрастающей (строго убывающей) на промежутке X, если большему значению аргумента соответствует большее (меньшее) значение функции. Более точно, функция у=f(x) называется строго возрастающей (строго убывающей) на промежутке X, если для любых двух значений х1 и х2, принадлежащих этому промежутку из неравенства х2>х1 следует неравенство f(х2)>f(х1) (f(х2)<f(х1)).

Строго возрастающие и строго убывающие функции называются строго монотонными функциями.

Если последнее неравенство является нестрогим, то говорят о нестрогом возрастании (нестрогом убывании) функции или просто о возрастании (убывании) функции.

Опр. 3. Функция у=f (х) называется возрастающей (убывающей) на промежутке X, если для любых двух значений х1 и х2, принадлежащих этому промежутку из неравенства х2>х1 следует нестрогое неравенство f(х2)≥f(х1) (f(х2)≤f(х1))

Возрастающие и убывающие функции называются монотонными функциями.

Ограниченность.

Опр. 4. Функция называется ограниченной на промежутке X, если существует такое положительное число М>0, что |f(x)|<М для любого х X.

Периодичность.

Опр. 5. Функция у=f(x) называется периодической, если существует положительное число Т такое, что f(х+Т)=f(x). Наименьшее число с таким свойством называется периодом функции.

Для построения графика периодической функции достаточно изобразить его на отрезке, длина которого равна периоду (основная область), а затем построить периодическое продолжение графика, повторяя график, нарисованный в основной области.