Каноническое уравнение прямой в пространстве. Уравнение прямой, проходящей через две заданные точки.
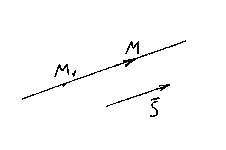
Пусть М1(x1, y1, z1) – точка, лежащая
на прямой l, и 
–
её направляющий вектор. Вновь возьмём
на прямой произвольную точку М(x,y,z) и
рассмотрим вектор 
.
Ясно, что векторы 
и 
коллинеарные,
поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,
– канонические уравнения
прямой.
Замечание 1. Заметим, что канонические
уравнения прямой можно было получить
из параметрических,исключив параметр t.
Действительно, из параметрических
уравнений почем 
или
.
Угол между двумя прямыми в пространстве. Условие параллельности и перпендикулярности прямых. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости.
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен .
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Р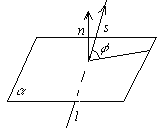
ассмотрим
векторы
и 
.
Если угол между ними острый, то он
будет 
,
где φ – угол между прямой и плоскостью.
Тогда 
.
Если угол между векторами 
и
тупой,
то он равен 
.
Следовательно 
.
Поэтому в любом случае 
.
Вспомнив формулу вычисления косинуса
угла между векторами, получим 
.
Условие перпендикулярности прямой и
плоскости. Прямая и плоскость
перпендикулярны тогда и только тогда,
когда направляющий вектор прямой
и
нормальный вектор
плоскости
коллинеарны, т.е. 
.
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
Канонические уравнения окружности, эллипса, гиперболы, параболы.
каноническое уравнение окружности: (х – х0)2 + (у – у0)2 = R2.
каноническое уравнение эллипса
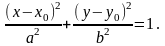
здесь точка А(х0,у0) - центр эллипса, а и b - большая и малая полуоси эллипса.
каноническое уравнение гиперболы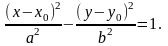
где точка А(х0у0) - центр гиперболы, а и b — действительная и мнимая полуось.
эта фигура обладает одной осью симметрии. Если директриса параболы перпендикулярна оси Ох, то уравнение кривой имеет вид (у – у0)2 = 2р(х – х0),
где р - расстояние от фокуса до директрисы.
Поверхности второго порядка.
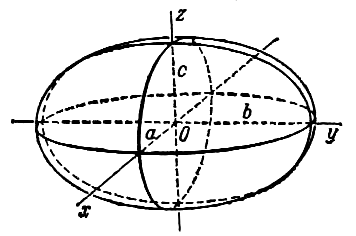
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c - сжатым. В случае, когда a=b=c, эллипсоид представляет собой сферу.
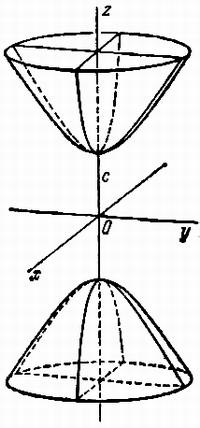
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
,
(2)
.
(3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), - двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
,
(4)
,
(5)
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), - гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
