33. Первый замечательный предел.

Первый замечательный предел , он раскрывает неопределенность (0/0).

34. Второй замечательный предел. Число е.

Второй замечательный предел

35. Задачи, приводящие к понятию производной. Геометрический и физический смысл производной. Уравнение касательной к кривой.

Опр. 1. Пусть функция у=f(х) определена в точке х0 и некоторой ее окрестности, придадим точке х0 приращение Δх и получим точку х0+Δх, значение функции в этой точке – f(х0+Δх). Разность значений f(х0+Δх) – f(х0) называется приращением функции, обозначается приращение функции Δf или Δу, т.е. Δf=f(х0+Δх) – f(х0).

Опр. 2. Производная функция у=f(х), в точке х0 определяется как предел отношения приращения функции Δу к приращению аргумента Δх, при стремлении Δх к нулю. Обозначается f `(x0) = lim (Δf/Δx).

Для вычисления производной выведены правила нахождения производной и таблицы производных элементарных функций.

Опр. 3. Функция, имеющая производную в точке х, называется дифференцируемой в этой точке.

Опр. 4. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале.

Геометрический смысл производной заключается в том, что производная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

Физический смысл. Производная - это скорость изменения функции в точке x. Из определения производной следует, что f’(x) Δf/Δx, причем точность этого приближенного равенства тем выше, чем меньше Δx. Производная f’(x) является приближенным коэффициентом пропорциональности между Δf и Δx

36. Дифференциал функции в точке, его геометрический смысл. Правила вычисления дифференциала.

Р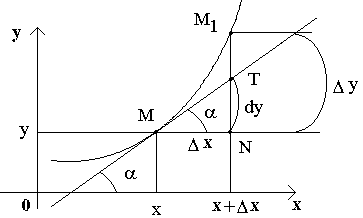 ассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка

M1(x+Δx; y+Δy).

Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.

Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.

Пусть U(х) и V(х) дифференцируемы в точке х.

(U(x) + V(x))` = U`(x) + V`(x)

(U(x) · V(x))` = U`(x) · V(x) + V`(x) · U(x)

(C·U(x))` = CU`(x), C - const

(U(x) / V(x))` = [U`(x) · V(x) - V`(x) · U(x)]/ V2(x).

37. Связь между дифференцируемостью и непрерывностью функции в точке.

Теорема. Если функция имеет производную в точке, то она непрерывна в этой точке.

Формула для нахождения производной от сложной функции такова:

[f (φ(х))]` = fφ`(φ(x)) ·φ`(x)

Дифференцирование обратной функции. Если у=f(x) и х=g(y) – взаимно-обратные дифференцируемые функции и у'х≠0, то т. е. производная обратной функции равна обратной величине производной данной функции.