3 Побудова графіків динамічних характеристик системи

Науковий аналіз та синтез САК оснований на використанні динамічних характеристик.

Динамічні характеристики описують як поведінку системи в цілому, так і поведінку окремих її елементів під час роботи системи, тобто, під час перехідних процесів [3, 8].

Динамічні характеристики можуть бути задані у вигляді:

1. диференціального рівняння в часі;

2. передаточної функції на комплексній площині;

3. перехідних процесів як реакцій на певні збурення, що мають аперіодичну форму;

4. функцій частоти , які називають частотними характеристиками.

В деяких випадках динамічні характеристики можуть бути визначені аналітичним шляхом на основі аналізу процесів, що протікають в елементі або системі, котрі розглядаються [4].

Один з методів аналітичного дослідження полягає в тому, що складна система розбивається на простіші елементи, для яких складаються диференціальні рівняння – математична модель у часі. Сукупність диференціальних рівнянь окремих елементів дає можливість визначити динамічні характеристики системи керування в цілому.

Цей метод на практиці має невелике застосування через недостатню вивченість та відсутність точного аналітичного опису багатьох технологічних процесів.

В разі неможливості або недоцільності аналітичного визначення динамічних характеристик системи вони отримуються дослідним шляхом.

Експериментальне дослідження також, як і аналітичне, може здійснюватись шляхом експериментального знаходження динамічних характеристик окремих елементів, по яких знаходять характеристики усієї системи.

Інший дослідний підхід полягає в експериментальному визначенні динамічних характеристик складної системи в цілому. Перевага цього підходу полягає в більшій достовірності отриманих характеристик, недолік – у відсутності даних про динамічні характеристики окремих елементів, що ускладнює аналіз та керування системи.

Як правило, поелементне дослідження динамічних властивостей застосовують до регулюючої частини САК, а об’єкти керування досліджуються в цілому.

3.1 Передаточна функція замкнутої системи

Згідно індивідуального завдання на курсову роботу після отримання передаточної функції досліджуваного чотириполюсника наступним кроком є знаходження передаточної функції замкнутої системи шляхом згортання структурної схеми, приведеної на рисунку 5.

Рисунок 5 – Структурна схема досліджуваної замкнутої системи

Зображення САК у вигляді сукупності динамічних ланок із вказівкою зв'язків між ними називають структурною схемою САК. Структурна схема САК дає наочне уявлення про зв'язки між ланками, про проходження та перетворення сигналів. Структурна схема може бути складена на основі відомих рівнянь системи, і, навпаки, рівняння системи можуть бути отримані за структурною схемою. Перша задача може мати різні варіанти розв’язання (різні структурні схеми), а друга вирішується однозначно. Передбачається, що динамічні ланки мають односпрямовану дію (від входу до виходу) і не впливають на інші, з'єднані з ними, ланки (не змінюють їхні передаточні функції) [11].

САК, як правило, є замкненими системами. Але при їхньому проектуванні часто попередньо розглядається розімкнуте коло ланок, яке потім замикається. Розглянемо спочатку передаточні функції розімкнутого кола ланок та, зокрема, правила структурних перетворень, які дозволяють в результаті їх застосування отримувати рівняння типових схем з’єднання ланок.

Коло із послідовно з'єднаних ланок. Типове послідовне зєднання декількох динамічних ланок показано на рисунку 6.

Рисунок 6 – Послідовне з’єднання ланок

Передаточна функція такого кола дорівнює добутку передаточних функцій усіх ланок, тобто

. (19)

Коло із паралельно з'єднаних ланок. Типове паралельне з’єднання декількох динамічних ланок показано на рисунку 7.

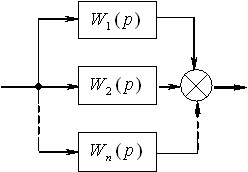
Рисунок 7 – Паралельне з’єднання ланок

Передаточна функція розімкнутого кола із паралельно з'єднаних ланок буде дорівнювати сумі передаточних функцій цих ланок:

. (20)

Коло з місцевим зворотним зв’язком. Типове з’єднання декількох динамічних ланок із застосуванням місцевого зворотного зв’язку показано на рисунку 8 [5, 11].

Рисунок 8 – Типове з’єднання ланок із місцевим зворотним звязком

Зворотний зв'язок (ЗЗ) може бути позитивним (+) або негативним (-). Результуюча передаточна функція для кожного із випадків запишеться наступним чином:

(21)

У формулі (21) знак “–” відноситься до позитивного, а знак “+” – до негативного ЗЗ. Головне застосування в САК мають негативні зворотні зв'язки.

Якщо в якості зворотного зв’язку застосовується підсилювач, то такий зв'язок називається жорстким, якщо , то зв'язок називається одиничним жорстким. Якщо з виходу на вхід системи подається не сама вхідна величина, а похідна від неї, то зв'язок називається гнучким. Гнучкий зв'язок діє тільки у перехідному режимі, а в сталому режимі він сам по собі відключається тому, що похідна від константи = 0.

В загальному випадку складне розімкнуте коло ланок може містити у собі комбінації всіх трьох розглянутих випадків. Структурна схема індивідуального завдання, приведена на рисунку 5, як раз містить кожен із різновидів типового зєднання ланок. Використовуючи вище наведені правила для структурних з’єднань, можна знайти загальну передаточну функцію досліджуваної в курсовій роботі структурної схеми.