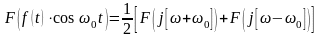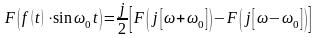- •Раздел 1: Элементы Теории Сигналов Параграф 1.1: Классификация сигналов.
- •Параграф 1.2: Пространство векторов и сигналов.
- •1.2.1: Общие сведения. Определение линейного векторного пространства.
- •1.2.2: Линейная независимость, размерность и базис линейного пространства.
- •1.2.3: Метрические и нормированные пространства. Скалярные произведения.
- •1.2.4: Функциональные пространства Евклида, Гильберта, Хемминга.
- •1.2.5: Операторы и функционалы.
- •1.2.6: Ортогональность элементов в пространстве.
- •1.2.7: Разложение сигналов в обобщенный ряд Фурье. Равенство Парсеваля
- •Параграф 1.3: Спектральное представление сигналов
- •Параграф 1.4: Тригонометрический ряд Фурье
- •Параграф 1.5: Комплексная и экспонентациальная форма представления ряда Фурье.
- •Параграф 1.6: Разложение в ряд Фурье периодическую функцию. Временное и частотное представление сигнала.
- •Параграф 1.7: Преобразования Фурье.
- •Параграф 1.8: Свойства преобразования Фурье.
- •Параграф 1.9: Сообщения, сигналы и помехи как случайные процессы. Параграф 1.9.1: Понятие случайного процесса.
- •Параграф 1.9.2: Вероятностное описание случайного процесса.
- •Параграф 1.9.3: Моментные функции случайных процессов.
- •Параграф 1.9.4: Стационарные случайные процессы.
- •Параграф 1.9.5: Эргодические случайные процессы.
- •Параграф 1.9.6: Случайные процессы, определяемые двумерной плотностью вероятности.
- •Параграф 1.9.7: Энергетический спектр случайного процесса.
- •Параграф 1.9.8: Теорема Винера - Хинчина.
- •Параграф 1.9.9: Квазибелый и белый шум.
- •Параграф 1.10: Комплексное и квазигармоническое представление сигналов. Параграф 1.10.1: Комплексное представление детерминированных сигналов.
- •Параграф 1.10.2: Комплексные случайные процессы.
- •Параграф 1.10.3: Огибающая и фаза комплексного случайного процесса. Квазигармоническое представление случайных процессов.
- •Параграф 1.10.4: Комплексная огибающая. Синфазная и квадратурная составляющая сигнала.
- •Параграф 1.10.5: Вероятностные характеристики огибающей фазы случайного процесса.
- •Раздел 2: Каналы электросвязи Параграф 2.1: Определение классификации каналов связи.
- •Параграф 2.2: Искажения и помехи в каналах связи.
- •Параграф 2.3: Математические модели каналов связи.
- •Параграф 2.3.1.: Математические модели непрерывных каналов.
- •Параграф 2.3.2: Канал с аддитивным шумом или гауссовский канал.
- •Параграф 2.3.3: Канал с неопределенной фазой сигнала.
- •Параграф 2.3.4: Канал с замиранием.
- •Параграф 2.3.5: Канал с межсимвольной интерференцией (мси) и аддитивным шумом.
- •Параграф 2.3.6: Математические модели дискретных и дискретно-непрерывных каналов.
- •Параграф 2.4: Преобразование сигналов в линейных и нелинейных звеньях каналов связи Параграф 2.4.1: Звенья каналов связи как физические системы и их математические модели. Классификация систем.
- •Параграф 2.4.2:Описание поведения линейных систем во временной области Параграф 2.4.2.1: Импульсная характеристика, интеграл Дюамеля, дифференциальные уравнения системы.
- •Параграф 2.4.2.2:Метод переменных состояний
- •Параграф 2.4.3:Описание поведения линейных систем в частной области
- •Параграф 2.4.4: Передаточная функция линейной системы
- •Параграф 2.4.5:Минимально-фазовые и неминимально-фазовые системы
- •Параграф 2.4.6.1: Основные принципы синтеза аналоговых электрических фильтров
- •Параграф 2.4.6.2: Синтез фнч
- •Параграф 2.4.6.3: Проектирование фвч и пф
- •Параграф 2.5: Нелинейные системы
- •Параграф 2.6: Параметрические системы
- •Параграф 2.7: Прохождение случайных сигналов, через линейные, параметрические и нелинейные системы Параграф 2.7.1: Прохождение случайных сигналов линейные параметрические системы. Общие сведения.
- •Параграф 2.7.2: Определение корреляционной функции отклика y4(t) линейной параметрической системы со случайной характеристикой при случайном входном воздействии
- •Параграф 2.7.3: Определение корреляционной функции отклика y3(t)
- •Параграф 2.7.4: Определение корреляционной функции отклика y2(t)
- •Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)
- •Параграф 2.7.6: Определение распределения вероятностей отклика линейной системы на случайное входное воздействие
- •Параграф 2.7.7: Прохождение случайных воздействий через нелинейные системы
- •Раздел 3: Модуляция Параграф 3.1: Общие сведения.
Параграф 1.7: Преобразования Фурье.
С помощью экспонентациального или тригонометрического ряда Фурье можно представить либо периодическую функцию на интервале , либо временную на интервале . Желательно было бы иметь любую периодическую или непериодическую функцию на бесконечном интервале. Для решения этой задачи рассмотрим финитную функцию fT(t) длительностью Т, которая может быть представлена в виде экспонентациального ряда Фурье
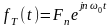 (*)
(*)
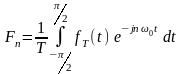 (**)
(**)
Введем новые обозначения:
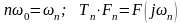
С их учетом (*) и (**) представим в виде:
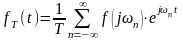 (***)
(***)
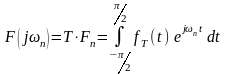 (4*)
(4*)
Подставив
в формулу (***)
 ,
получим:
,
получим:
 (5*)
(5*)
Предположим
теперь, что
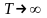 .
С увеличением Т уменьшается
.
С увеличением Т уменьшается
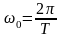 (частота первой гармоники), спектр
становится плотнее. Как видно из (**),
амплитуда Fn
отдельных спектральных составляющих
при этом уменьшается, но форма частотного
спектра, определяемая соотношением
этих составляющих, остается неизменной.
В пределе при
(частота первой гармоники), спектр
становится плотнее. Как видно из (**),
амплитуда Fn
отдельных спектральных составляющих
при этом уменьшается, но форма частотного
спектра, определяемая соотношением
этих составляющих, остается неизменной.
В пределе при
![]() амплитуда спектральных составляющих
становится бесконечно малыми, но при
этом частоты спектральных составляющих
приближаются друг к другу (
амплитуда спектральных составляющих
становится бесконечно малыми, но при
этом частоты спектральных составляющих
приближаются друг к другу (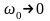 ,
они отличаются на
).
Спектр существует на любой
частоте, и из дискретных функций частоты
превращаются в непрерывный. При этом
(5*) и (4*) преобразуются:
,
они отличаются на
).
Спектр существует на любой
частоте, и из дискретных функций частоты
превращаются в непрерывный. При этом
(5*) и (4*) преобразуются:
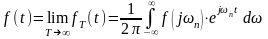 (6*)
(6*)
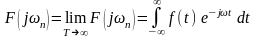 (7*)
(7*)
Выражения
(6*) и (7*) называются соответственно
обратным и прямым преобразованием
Фурье. Равенство (6*) представляет
непериодическую функцию f(t)
как непрерывную сумму экспонентациальных
функций с частотами из интервала
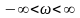 .
Амплитуда составляющей на любой частоте
.
Амплитуда составляющей на любой частоте
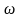 пропорциональна
пропорциональна
 ,
поэтому
характеризует плотность распределения
функции f(t)
по
частотам гармоник, и называется функцией
спектральной плотности. Если исследуем
сигнал напряжения, то
имеет размерность
,
поэтому
характеризует плотность распределения
функции f(t)
по
частотам гармоник, и называется функцией
спектральной плотности. Если исследуем
сигнал напряжения, то
имеет размерность
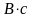 .
Из выражения (7*) видно, что
является комплексной функцией частоты,
поэтому её называют комплексным спектром
сигнала f(t).
Модуль
.
Из выражения (7*) видно, что
является комплексной функцией частоты,
поэтому её называют комплексным спектром
сигнала f(t).
Модуль
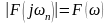
называется спектром амплитуд, а аргумент
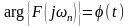
–
спектром
фаз. Если бы в исходной функции наших
рассуждений мы записали бы разложение
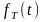 не в экспонентациальном, а тригонометрическом
ряде Фурье, то аналогичным образом могли
бы прийти к понятиям действительных
спектральных плотностей
не в экспонентациальном, а тригонометрическом
ряде Фурье, то аналогичным образом могли
бы прийти к понятиям действительных
спектральных плотностей
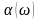 и
и
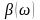 :
результатов аналогичных предельных
переходов коэффициентов an
и bn
тригонометрического ряда Фурье. Так же
приведенные преобразования могут быть
выполнены по отношению к другим базисным
функциям, что позволяет распределить
разложение функции в обобщенный ряд
Фурье на бесконечном интервале.
:
результатов аналогичных предельных
переходов коэффициентов an
и bn
тригонометрического ряда Фурье. Так же
приведенные преобразования могут быть
выполнены по отношению к другим базисным
функциям, что позволяет распределить
разложение функции в обобщенный ряд
Фурье на бесконечном интервале.
Параграф 1.8: Свойства преобразования Фурье.
Приведем
без доказательства основные свойства
преобразования Фурье. Введем обозначения
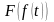 – преобразования Фурье функции f(t).
– преобразования Фурье функции f(t).
Свойство линейности: если
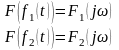 ,
то
,
то
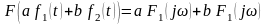 .
.Свойство изменения масштаба: если
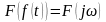 ,
то для любой действительной постоянной
а
преобразования Фурье:
,
то для любой действительной постоянной
а
преобразования Фурье:
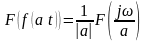 .
.Свойство частотного сдвига: если , то
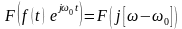
Следствие из 3 свойства:
Свойство временного сдвига: если , то
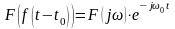 .
.Дифференцирование и интегрирование во времени: если , то
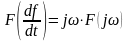 ;
;
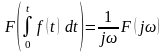 .
.Теорема о свертке: если
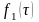 и
и
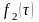 ,
т.е.
,
т.е.
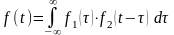 (это свертка), то преобразование Фурье
от
(это свертка), то преобразование Фурье
от
 :
:
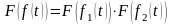 (в частотной области).
(в частотной области).Теорема произведения: если ,
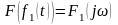 ,
,
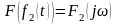 ,
,
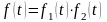 ,
то
,
то
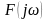 представляет собой свертку спектров
представляет собой свертку спектров
 и
и
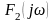 ,
т.е.
,
т.е.
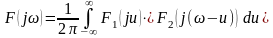 (
(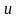 имеет
размерность частоты).
имеет
размерность частоты).
Замечание:
Если
в качестве аргументов спектральной
плотности фигурирует не круговая, а
обычная частота
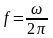 ,
то множитель
,
то множитель
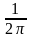 в последнем выражении отсутствует.
в последнем выражении отсутствует.