Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)

Корреляционную функцию отклика y₁(t) детерминированной линейной системы с характеристикой 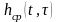на детерминированное входное воздействие m_x(t) можно определить с помощью (16), если учесть соотношения (17, 18):

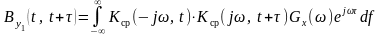(25)

Если параметры системы не меняются во времени (если система стационарна), то

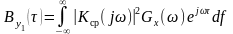(26)

Энергетический спектр выхода: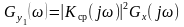 (27)

Учитывая, что 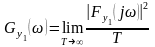и (18) для спектров амплитуд входа 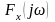и выхода 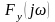получаем из (27) известное ранее:

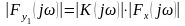
Параграф 2.7.6: Определение распределения вероятностей отклика линейной системы на случайное входное воздействие

Задача нахождения распределения вероятностей отклика линейной системы при произвольном случайном воздействии в общем случае оказывается весьма сложной даже при определении одномерного распределения, поэтому ограничимся рассмотрением лишь некоторых частных случаев. Если на вход линейной детерминированной системы подан Гауссовский процесс, то и процесс на выходе остается Гауссовским, что следует из известных свойств нормального распределения, которое остается нормальным при любых линейных преобразованиях. Если полоса частот Fc, занимаемая входным сигналом X(t) много шире полосы пропускания Fпр данной линейной системы, то распределения выходного процесса имеют тенденцию приближаться к нормальному независимо от вида распределения входного сигнала. Это можно объяснить из (П*) исходя из соотношения . Приближенно соотношение можно представить в виде суммы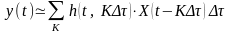 (28), где шаг дискретизации по 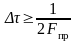 (см. теорему Котельникова)

— ширина спектра импульсной характеристики системы

Если ширина энергетического спектра входного процесса F_c по сравнению с F_пр, то время корреляции _к этого процесса много меньше интервала . В этом случае всякие две случайные величины 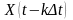и 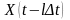как сечение процесса x(t) можно считать практически независимыми и к сумме (28) можно применить центральную предельную теорему. Согласно этой теореме распределение вероятностей суммы независимых случайных величин (сумма (28)), а следовательно, интегралу (n*) будет стремиться к нормальному, причем будет тем ближе к нормальному, чем больше слагаемых в этой сумме. В нашем случае распределение суммы (28) будет тем ближе к нормальному, чем больше отношение ширины спектра входного сигнала к полосе пропускания цепи. В предельном случае, если на входе цепи действует белый шум, у которого ширина спектра бесконечна, а цепь имеет неограниченную полосу пропускания, то выходной процесс будет строго Гауссовским. В других случаях, если процесс на входе системы не Гауссовский, то на выходе линейной системы его распределение меняется весьма существенно. Весьма прост определяется распределение процесса на выходе безынерционных параметрических систем, вход и выход которых связаны зависимостью вида . 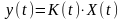Если K(t) — детерминированная функция, то в виду взаимооднозначной связи x(t) и y(t) имеет место следующее соотношение между одномерными распределениями входного 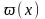и выходного 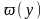процесса.

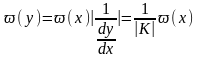
Если K(f) функция случайная, то распределение y(t) находится как распределение произведения случайных процессов.