
- •Раздел 1: Элементы Теории Сигналов Параграф 1.1: Классификация сигналов.
- •Параграф 1.2: Пространство векторов и сигналов.
- •1.2.1: Общие сведения. Определение линейного векторного пространства.
- •1.2.2: Линейная независимость, размерность и базис линейного пространства.
- •1.2.3: Метрические и нормированные пространства. Скалярные произведения.
- •1.2.4: Функциональные пространства Евклида, Гильберта, Хемминга.
- •1.2.5: Операторы и функционалы.
- •1.2.6: Ортогональность элементов в пространстве.
- •1.2.7: Разложение сигналов в обобщенный ряд Фурье. Равенство Парсеваля
- •Параграф 1.3: Спектральное представление сигналов
- •Параграф 1.4: Тригонометрический ряд Фурье
- •Параграф 1.5: Комплексная и экспонентациальная форма представления ряда Фурье.
- •Параграф 1.6: Разложение в ряд Фурье периодическую функцию. Временное и частотное представление сигнала.
- •Параграф 1.7: Преобразования Фурье.
- •Параграф 1.8: Свойства преобразования Фурье.
- •Параграф 1.9: Сообщения, сигналы и помехи как случайные процессы. Параграф 1.9.1: Понятие случайного процесса.
- •Параграф 1.9.2: Вероятностное описание случайного процесса.
- •Параграф 1.9.3: Моментные функции случайных процессов.
- •Параграф 1.9.4: Стационарные случайные процессы.
- •Параграф 1.9.5: Эргодические случайные процессы.
- •Параграф 1.9.6: Случайные процессы, определяемые двумерной плотностью вероятности.
- •Параграф 1.9.7: Энергетический спектр случайного процесса.
- •Параграф 1.9.8: Теорема Винера - Хинчина.
- •Параграф 1.9.9: Квазибелый и белый шум.
- •Параграф 1.10: Комплексное и квазигармоническое представление сигналов. Параграф 1.10.1: Комплексное представление детерминированных сигналов.
- •Параграф 1.10.2: Комплексные случайные процессы.
- •Параграф 1.10.3: Огибающая и фаза комплексного случайного процесса. Квазигармоническое представление случайных процессов.
- •Параграф 1.10.4: Комплексная огибающая. Синфазная и квадратурная составляющая сигнала.
- •Параграф 1.10.5: Вероятностные характеристики огибающей фазы случайного процесса.
- •Раздел 2: Каналы электросвязи Параграф 2.1: Определение классификации каналов связи.
- •Параграф 2.2: Искажения и помехи в каналах связи.
- •Параграф 2.3: Математические модели каналов связи.
- •Параграф 2.3.1.: Математические модели непрерывных каналов.
- •Параграф 2.3.2: Канал с аддитивным шумом или гауссовский канал.
- •Параграф 2.3.3: Канал с неопределенной фазой сигнала.
- •Параграф 2.3.4: Канал с замиранием.
- •Параграф 2.3.5: Канал с межсимвольной интерференцией (мси) и аддитивным шумом.
- •Параграф 2.3.6: Математические модели дискретных и дискретно-непрерывных каналов.
- •Параграф 2.4: Преобразование сигналов в линейных и нелинейных звеньях каналов связи Параграф 2.4.1: Звенья каналов связи как физические системы и их математические модели. Классификация систем.
- •Параграф 2.4.2:Описание поведения линейных систем во временной области Параграф 2.4.2.1: Импульсная характеристика, интеграл Дюамеля, дифференциальные уравнения системы.
- •Параграф 2.4.2.2:Метод переменных состояний
- •Параграф 2.4.3:Описание поведения линейных систем в частной области
- •Параграф 2.4.4: Передаточная функция линейной системы
- •Параграф 2.4.5:Минимально-фазовые и неминимально-фазовые системы
- •Параграф 2.4.6.1: Основные принципы синтеза аналоговых электрических фильтров
- •Параграф 2.4.6.2: Синтез фнч
- •Параграф 2.4.6.3: Проектирование фвч и пф
- •Параграф 2.5: Нелинейные системы
- •Параграф 2.6: Параметрические системы
- •Параграф 2.7: Прохождение случайных сигналов, через линейные, параметрические и нелинейные системы Параграф 2.7.1: Прохождение случайных сигналов линейные параметрические системы. Общие сведения.
- •Параграф 2.7.2: Определение корреляционной функции отклика y4(t) линейной параметрической системы со случайной характеристикой при случайном входном воздействии
- •Параграф 2.7.3: Определение корреляционной функции отклика y3(t)
- •Параграф 2.7.4: Определение корреляционной функции отклика y2(t)
- •Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)
- •Параграф 2.7.6: Определение распределения вероятностей отклика линейной системы на случайное входное воздействие
- •Параграф 2.7.7: Прохождение случайных воздействий через нелинейные системы
- •Раздел 3: Модуляция Параграф 3.1: Общие сведения.
1.2.3: Метрические и нормированные пространства. Скалярные произведения.
Метрическим
называется линейное пространство, в
котором определено расстояние (метрика)
между элементами (векторами) пространства,
т.е. каждой паре элементов x
и y
поставлено
в соответствие некоторое действительное
вещественное неотрицательное число
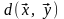 и указан способ, в соответствие с которым
и находится это число.
и указан способ, в соответствие с которым
и находится это число.
Расстояние удовлетворяет следующим условиям:
 ,
если
,
если
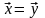
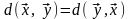
 ,
где
,
где
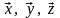 – элементы (точки) пространства.
– элементы (точки) пространства.
Третье условие называется неравенством треугольника. Длина стороны треугольника меньше или равна сумме длин двух других сторон.
Важным
классом линейных метрических пространств
является линейное нормированное
пространство (ЛНП). Линейное пространство
является нормированным унитарным, если
для каждого элемента
существует неотрицательное число
 ,
называемое его нормой, которое
удовлетворяет условиям:
,
называемое его нормой, которое
удовлетворяет условиям:
= 0, при
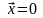
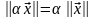 ,
где
,
где
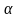 – скаляр.
– скаляр. .
.
Введение
нормы позволяет сравнивать векторы по
значению, т.е. норма представляет собой
численную оценку (длину) вектора.
Метрические линейные пространства
(МЛП) называют банаховым пространством.
В линейном пространстве можно
аксиоматически ввести понятие скалярного
произведения
 (двух элементов).
(двух элементов).
Скалярным произведением является число (в общем случае, комплексное), удовлетворяющее следующим условиям:
 ,
где * – комплексное произведение.
,
где * – комплексное произведение. при
при
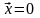
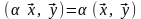

1.2.4: Функциональные пространства Евклида, Гильберта, Хемминга.
Вещественным
Евклидовым пространством Rn
называется линейное n-мерное
векторное пространство, любой вектор
которого определяется совокупностью
конечного числа n
его действительных координат
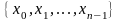 как
как
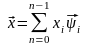 (*1), где
(*1), где
 -
единичный базисный вектор. Пространство
Rn
можно определить как множество точек,
представленных концами векторов, для
которых
-
единичный базисный вектор. Пространство
Rn
можно определить как множество точек,
представленных концами векторов, для
которых
 ,
где
,
где
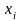 – координаты вектора. При n
= 2, n
= 3 Евклидово пространство представляет
собой обобщение соответственно
двухмерного и трехмерного пространств
геометрических векторов, в которых
норма имеет смысл длины вектора.
Расстояние между двумя векторами
и
– координаты вектора. При n
= 2, n
= 3 Евклидово пространство представляет
собой обобщение соответственно
двухмерного и трехмерного пространств
геометрических векторов, в которых
норма имеет смысл длины вектора.
Расстояние между двумя векторами
и
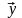 определяется как норма разностей
векторов:
определяется как норма разностей
векторов:
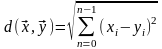
Скалярное произведение в этом пространстве определяется как:
 ,
,
где φ- угол между векторами и .
Зримо, этот угол может быть представлен в пространстве геометрических векторов при n = 2, n = 3. Для проекции вектора на и обратно имеем:
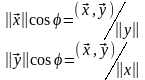
Координаты вектора xi в (*1) представляет собой его проекции на направление координат осей, т.е на векторы базиса . Из определения скалярного произведения вытекает неравенство Бунеаковского – Шварца:

Знак
равенства имеет место, когда
 ,
где k
– скаляр, когда векторы
и
коллениарны. Для соответствующих сигналы
x(t)
и y(t)
это означает, что они совпадают по форме.
При
Rn
переходит в бесконечномерное пространство
Гильберта L2.
Гильбертово пространство в частности
пространство непрерывных комплексных
функций действительного аргумента T,
заданных на интервале (–T/2;
T/2),
в котором скалярное произведение
определено соответствием:
,
где k
– скаляр, когда векторы
и
коллениарны. Для соответствующих сигналы
x(t)
и y(t)
это означает, что они совпадают по форме.
При
Rn
переходит в бесконечномерное пространство
Гильберта L2.
Гильбертово пространство в частности
пространство непрерывных комплексных
функций действительного аргумента T,
заданных на интервале (–T/2;
T/2),
в котором скалярное произведение
определено соответствием:
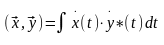
где
 – комплексная функция времени, а знак
«*» – комплексное сопряжение.
– комплексная функция времени, а знак
«*» – комплексное сопряжение.
Квадрат нормы в пространстве L2:
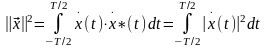
Эта
величина имеет не только геометрический,
но и физический смысл. Если действительный
сигнал x
(t)
электрический ток в единичном сопротивлении
1 Ом, то
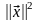 определяет энергию сигнала Ex:
определяет энергию сигнала Ex:
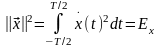
Элементы Гильбертова пространства L2 характеризуются интегрируемым квадратом, т.е., если элементы этого пространства – действительные сигналы x (t), определенные на интервале (–T/2; T/2), то выполняется условие:
 (*)
(*)
Гильбертово пространство при этом обозначается как L2 (T). При Т → ∞ получаем пространство L2 (∞). Для некоторых сигналов векторов пространства L2 (∞) условие (*) может не выполняться, но выполняется условие:
 (**)
(**)
В этом случае вводится скалярное произведение с размерностью мощности Рх (для токов и напряжений с единичным сопротивлением):
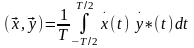 (***)
(***)
При этом квадрат нормы:
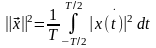 (****)
(****)
При выполнении условия (***) в пространстве L2 (∞) определены соотношения (***) и (****) при Т → ∞. Квадрат расстояния между двумя векторами в вещественном пространстве L2 (T) определяется соотношениями:

Пространство L2 представляет собой естественное обобщение пространства Rn, получаемое путем перехода от дискретной функции непрерывного аргумента. В курсе ТЭС пространство L2 имеет особое значение, т.к. оно позволяет применить общие геометрические представления к сообщениям, сигналам и помехам, определенным как функция непрерывного аргумента. Устремляя в (*1) n→ ∞, получаем представление x (t) в пространстве Гильберта:

Важную
роль в теории кодирования играет
пространство Хемминга, элементами
(векторами) которого являются двоичные
n-разрядные
кодовые комбинации
 .
.
Пример:

n=5
Сложение векторов в этом пространстве реализуется как поразрядное сложение элементов кодовой комбинации по модулю 2.

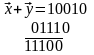
Пространство Хемминга определено над полем GF (2), т.е. множество скаляров, с которыми взаимодействует данное пространство, содержит 2 элемента – 1 или 0.
Скалярное произведение в этом пространстве задается как:

где сумма понимается в обычном смысле, а не по модулю 2. Отсюда норма двоичного вектора:
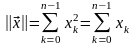
т.к. 12 =1 и 02 = 0.
Можно видеть, что норма двоичного вектора определяется количеством содержащихся в нем 1. Эту норму называют также весом вектора W. Расстояние в пространстве Хемминга:
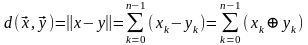 ,
,
где
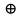 – суммирование по модулю 2.
– суммирование по модулю 2.
В поле GF (2) сложение по модулю 2 и вычитание по модулю 2 эквивалентно. Из этого определения следует, что в пространстве Хемминга расстояние между двоичными векторами определяется по числу позиций кодовой комбинации, в которых вектора имеют разные символы.
