Параграф 2.4.6.1: Основные принципы синтеза аналоговых электрических фильтров

Электрические фильтры, позволяющие осуществлять разделение сигналов по их спектру и представляющие собой линейные непрерывные системы, являются одним из наиболее важных узлов телекоммуникационной аппаратуры.

Рассмотрим основные принципы их проектирования.

Обычно при синтезе фильтров нижних частот (ФЧХ), ФВЧ и полосовых фильтров (ПФ) задаются желаемой формы АЧХ, а к ФЧХ не предъявляют каких-либо специфических требований. Предполагается, что обеспечение удовлетворительной равномерности АЧХ линейного функционального фильтра в заданной полосе частот. Одновременно также обеспечивает и линейность ФЧХ в этой полосе.

Синтез фильтра по заданной АЧХ начинается с того (1-ый этап), что выбирают некоторую идеализированную функцию, которая описывает частотную зависимость Кр(ω) коэффициента передачи мощности, равного квадрату АЧХ:

(*)

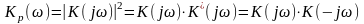В отличие от КЧХ К(jω) функция К_р(ω) действительна и поэтому удобна для анализа исходных данных к синтезу фильтра.

Если в выражении (*) подставить переменную р вместо jω, т.е. принять jω = р и тем самым перейти от КЧX к передаточной функции получим:

К_р(р) = К(р) К(-р) (**)

Формула (**) устанавливает следующий факт:

если 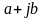— особая точка функции К(Р), то К_р(Р) будет иметь такую же особую точку, как при 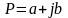, так и при .

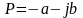Таким образом, особые точки передаточной функции мощности К_р(р) имеют квадрантную симметрию, т.е. располагаются на комплексной плоскости, имея центр симметрии в начале координат.

Это свойство дает возможность восстановить передаточную функцию К(р), а следовательно И АЧХ К(jω) по передаточной функции мощности К_р(р).

Как правило идеализированная характеристика Кр(ω) является физически реализуемой, поэтому 2-ой этап синтеза состоит в аппроксимации этой характеристики. Такой функцией, которая соответствует физически реализуемой системе. Наиболее распространенным типами аппроксимации являются:

- аппроксимация по полиномам Баттерворта

- полиномами Чебышева

- эллиптическими функциями

Затем третий этап переходят от К(ω) к Кр(р) и использую отмеченную выше симметрию особых точек, и находят передаточную функцию К(р) – фильтра.

По найденной передаточной функции К(р) выполняют четвертый этап синтеза заключающегося в реализации цепи, т.е. получении принципиальной схемы фильтра с номиналами входящих в него элементов.

Параграф 2.4.6.2: Синтез фнч

Рассмотрим как выполняются сформулированные рекомендации при синтезе ФНЧ.

Очевидно, что для ФНЧ с частотой среза ωс жалеемая идеализированная характеристика Кр(ω) имеет вид:

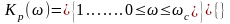
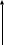Кр(ω)

1

Ω

Такая характеристика физически не реализуема, так как соответствующая ей К(ω) не отвечает критерием Пейли-Винера. Поэтому возникает задача подбора допустимой аппроксимируемой функции, которая может решаться разными способами. Один из способов ее решения основан на представлении характеристики K_p(ω) монотонной функцией вида:

, (*)

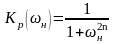где 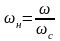- безмерная нормированная частота.

ФНЧ имеющий такие частотные свойства называется фильтром с максимально плоской характеристикой или фильтром Баттерворта. Целое число n=1,2,3… является периодом фильтра. Можно показать, что при любом n такой фильтр физически реализуем. Чем больше n, тем точнее аппроксимируется форма частотной характеристики.

Порядок фильтра подбирают обычно исходя из требований, предъявляемых к ослаблению сигналов с частотами w>1. Следующим этапом синтеза является определение полюсов передаточной функции K(Р), соответствующей выбранной форме (*) 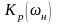. С этой целью, прежде всего, осуществляется переход от к K_p(Р), выполняемый в соответствии с правилом:

= K_p(Р)

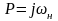, т.е. путем осуществления в (*) подстановки . При этом имеем 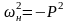  или 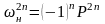 , поэтому с учетом (*) получаем:

(**)

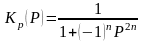Функция K_p(P) имеет 2n полюсов, являющихся решениями уравнения  . Можно показать, что все эти полюса определяются следующим выражением:

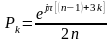где k=1,2,3...

Все эти полюсы расположены на окружности единичного радиуса на одинаковом угловом расстоянии друг от друга равном π/n.

Аргумент первого полюса 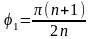последующего

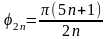
На рисунке показано расположение полюсов n=1 и n=2,

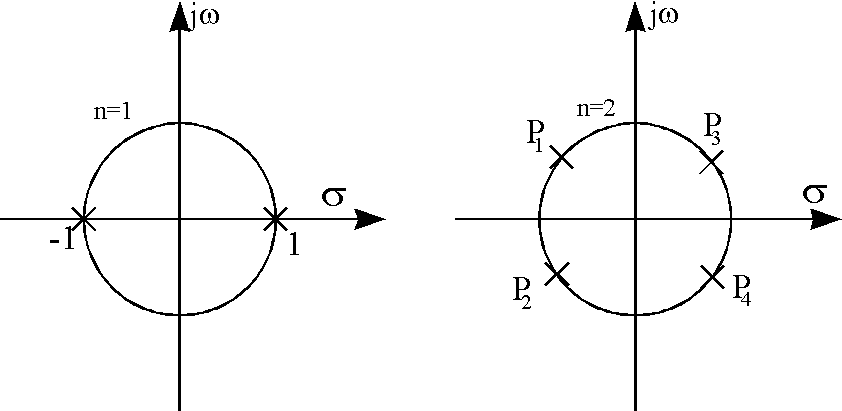
Определив все полюсы K_Р(Р) следует отобрать лишь те из них, которые расположились в левой полуплоскости, так как только в этом случае выполняется условие устойчивости фильтра, и считать их полюсами передаточной функции K(Р) синтезируемого фильтра. При этом выражение передаточной функции K(Р), например, для n=2 будет таким:

(***)

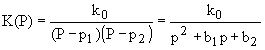Если n=3, то в знаменателе было бы три сомножителя, что соответствует полиному третьего порядка. Коэффициенты полиномов в знаменателе b1 и b2 и значение k0 обычно приводится в специальных таблицах пособиях по расчету фильтров. Для удовлетворительной аппроксимации идеальные характеристики ФНЧ с помощью функций Баттерворта требуют относительно высоких значений n. Для улучшенной аппроксимации этой характеристики часто применяется аппроксимация по Чебышеву, при которой Kp(wн) ФНЧ определяется следующей формулой:

(****)

где ε≤1 – постоянное число, называемое коэффициентом неравномерности АЧХ в полосе пропускания, а Tn(ω_н) - полином Чебышева n-го порядка, определяемый выражением :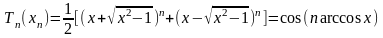

Полиномы Чебышева обладают следующими свойствами:

на интервале -1<х<1 они пульсируют вокруг нуля с амплитудой равной 1;

Тn(к)

-1 1 х

С помощью таких функций можно удачно аппроксимировать АЧХ ФНЧ. Из (****) видно, что в пределах полосы пропускания 0<ω_н<1 величина K_p(ω_н) будет изменяться в пределах  . Если же ωн>1, то фильтр обеспечивает большое затухание сигнала.

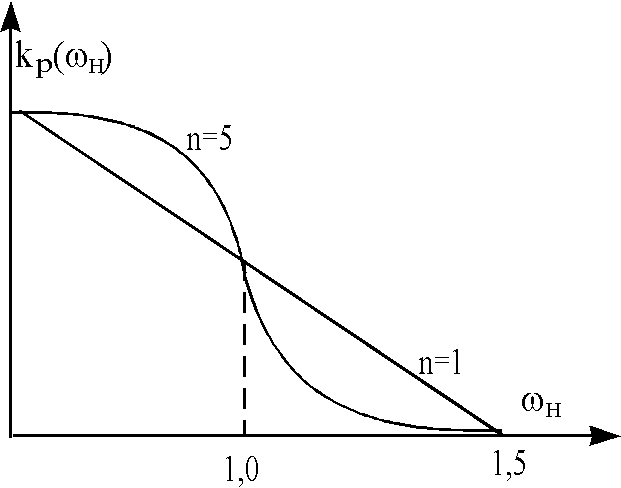
Фильтры Чебышева являются оптимальными в том смысле, что не существует какого-либо другого фильтра n-го порядка, содержащего такие полюсы, который имел бы такие же или лучшие характеристики и в полосе пропускания, и в полосе непропускания.

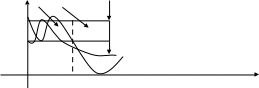
Графики зависимости K_p(ω_н) приведены на рисунке:

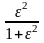
К_р(ω_н) n=1 n=3

1

ω_н=1 ω_н

Из графиков видно, что частотные характеристики фильтров Чебышева не монотонны. Существуют и другие способы аппроксимации идеальных фильтров ФНИ, обладающие другими достоинствами. Например, эллиптические фильтры характеризуются тем, что их имеет равновеликие пульсации и в полосе пропускания и в полосе непропускания. Эти фильтры являются оптимальными с точки зрения минимальной ширины переходной полосы, т.е. для заданных порядков фильтра и уровня пульсации обеспечивается наиболее быстрые переход от полосы пропускания к полосе непропускания. Однако передаточные функции таких фильтров кроме полюсов имеет и нули, что усложняет их реализацию.

Последний этап синтеза фильтра состоит в построении принципиальной схемы устройства и определения полиномов, входящих в схему устройства. Передаточную функцию К(Р) целесообразно представлять в виде произведения множителей, каждый из которых может являться передаточной функцией простейшего четырехполюсника. При этом комплексная характеристика такой цепи: , что соответствует последовательному включению звеньев с КЧХ ,

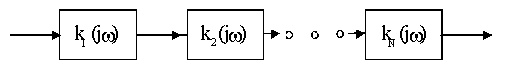
К(jω)

КЧХ должны быть такими, чтобы они реализовали те полюсы функции К(Р), которые были определены на этапе аппроксимации. Для создания фильтров требуются звенья двух видов. Звено первого порядка с единственным вещественным полюсом и звено второго порядка, имеющее пару комплексно сопряженных полюсов. Простейшим звеном первого порядка является, например, Г-образный четырехполюсник, для которого передаточная функция по напряжению  . Здесь  .

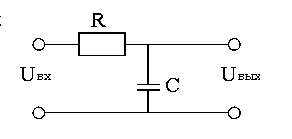
Звено второго порядка, имеющее два комплексно-сопряженных полюса также можно реализовать с помощью Г-образного четырехполюсника

,

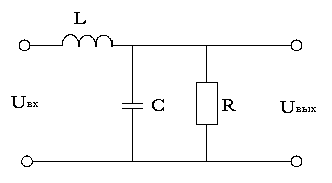
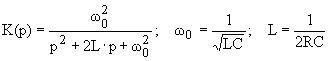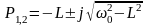
Приведенные здесь примеры реализации звеньев первого и второго порядка относятся к классу пассивных фильтров, характеризующихся тем, что их схемы не содержат усилительных элементов и состоят из набора определенным образом соединенных резисторов, конденсаторов и катушек индуктивности. Наличие последних обязательно для того, чтобы обеспечить возможность реализации передаточных функций с полюсами, лежащими не на осях координат комплексной плоскости, а в ее произвольных точках. Катушки индуктивности имеют большую массу, их трудно реализовать в интегральном исполнении. При их использовании появляются специфические погрешности. Все это обуславливает недостатки пассивных фильтров и ограничивает их применение. Независимыми они являются лишь там, где имеют место большие токи и напряжения. Наибольшее распространение получили активные фильтры, построенные на основе RC элементов и ОУ. При их использовании можно реализовать любые передаточные функции без катушек индуктивностей.