Параграф 2.4.2.2:Метод переменных состояний

При использовании соотношений связи между входными и выходными сигналами системы в виде интеграла Дюамеля для нахождения выходного сигнала помимо характеристик системы требуется знать так же входной сигнал, действовавший на всем промежутке его существования

(- ; t).

Описание модели непрерывных звеньев каналов связи дифференциальным уравнением позволяет всю предысторию до некоторого фиксированного момента времени t0 заменить заданием некоторого начального состояние системы (начальных условий), число которых равно порядку уравнения.

Зная характеристики системы (т.е. коэффициент уравнения), начальное состояние и сигнал, действующий только на интервале от t₀ до t₁, Можно последовательно определить как сигнал на выходе, так и новое состояние системы в любой момент времени t > t₀.

Такой подход лежит в основе метода переменных состояний.

При его реализации множество величин, однозначно определяющих поведение системы в некоторый момент t, содержащее min число элементов n (n – это порядок дифференциального уравнения системы), называется состоянием, сами элементы этого множества переменными состояния.

Значения этих переменных в момент t0 обычно задаются в виде начальных условий, определяющих исходное состояние системы.

Для того, чтобы сделать описание математической модели системы наиболее компактным прибегают к векторной (векторно-матричной) форме записи дифференциальных уравнений. При этом каждую из переменных состояния рассматривают как составляющую n – мерного вектора состояний.

Для любой системы можно составить 2 уравнения: одно из них позволяет по состоянию системы в момент t₀ и входному сигналу определить состояние в момент t > t0 (оно называется уравнением состояния), 2 – ое по тем же исходным данным (по состоянию в момент t₀ и входному сигналу) определяет выходной сигнал системы (оно называется уравнением наблюдения)

Рассмотрим введенные понятия на примере описания линейной системы, представляющей собой последовательный колебательный контур, изображенный на рисунке:

R L

i (t) C

Можно показать, что выходное напряжение У(t) такой системы связано с входным напряжением U(t) дифференциальным уравнением:

Состояние этой цепи в любой момент t0 характеризуется 2-мя параметрами:

- током i(t₀)

- и напряжением на емкости С У(t₀).

Значения i (t₀) и y(t₀) содержат достаточную информацию о предыстории цепи, связанной с прошлыми воздействиями U(t) при t ≤ t₀, которая необходима для определения будущих значений выходного процесса У(t) при заданном U(t) для t > t₀.

Таким образом, и y(t) можно рассматривать как переменные состояния, а дифференциальное уравнение системы как уравнение состояния.

Для того, чтобы записать его в форме векторного дифференциального уравнения 1-го порядка, произведем замену переменных.

Введем обозначения:

(*) x₁(t) = y(t)

x₂(t) =

При этом исходное дифференциальное уравнение 2-ого порядка эквивалентно системе 2-х дифференциальных уравнений 1-ого порядка.

( **)

C учетом правил векторно-матричных преобразований эта система может быть компактно записана в виде векторного дифференциального уравнения 1-го порядка:

(***)

где

У равнение наблюдения в данном случае имеет вид (*) или в векторной форме:

(****) У(t) = H x(t),

где H = [1 0].

О тметим, что выбранный вектор состояния x(t) не является единственно возможным. В качестве переменных состояния может быть выбраны, например напряжение на резисторе R и на индуктивности L.

Любое обратное линейное преобразование вектора приводит к другому вектору состояния.

Важной особенностью метода переменных состояния является возможность непосредственного моделирования систем, описываемых уравнениями состояния, с помощью аналогового или цифрового вычислительного устройства.

На следующем рисунке показана модель системы уравнений (**):

При построении такой схемы удобно рассуждать следующим образом:

Пусть в некоторых точках присутствуют входной сигнал U(t) и переменные состояния x₁(t) и x₂(t). Соединим эти точки сумматорами, усилителями и интеграторами, так, чтобы соотношения между ними соответствовали уравнению (**). Из 1-го уравнения следует, что подав на вход интегратора 2 x₂(t) получим с точностью до постоянной x₁(t).

Эта постоянная определяется начальным условием и равна x1 (t0).

Затем осуществляют операции, записанные в правой части 2-го уравнения системы, т.е. умножение U(t) и x₁(t) на , а x₂(t) на 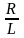(с помощью усилителей соответствия коэффициентами усиления) и сложим полученные результаты с учетом знаков.

Проинтегрировав полученную сумму в интеграторе 1 и прибавив к ней постоянную x₂(t₀) (начальное условие) получим x₂(t).

Таким образом все точки в схеме соединились в соответствии с уравнением (**). Если на такую схему модель подать входной сигнал U(t), то на выходе получится выходной сигнал y(t), однако это не представляет большого интереса поскольку то же самое можно сделать без моделирования, исследуя экспериментально исходную систему, изображенную на 1-ом рисунке; значительно важнее, что с помощью модели можно решить обратную задачу по выходному (т.е. наблюдаемому) сигналу найти входной, даже если выходной сигнал наблюдается на фоне шума.

В более общем случае аналогичные векторные уравнения в форме (***) и (****) можно построить для систем более высокого порядка, в том числе нелинейных и параметрических. Отличие будет лишь в размерности матриц и в том, что они могут быть функциями времени (для параметрических систем) и состояния (для нелинейных систем).

Если на систему воздействуют несколько входных, и она имеет несколько выходных сигналов, то их также рассматривают как компоненты вектора-функции.

В самом общем случае уравнение состояния и наблюдение процесса в векторной форме принимают следующий вид:

(уравнение состояния)

(уравнение наблюдения)

где – вектор шума наблюдения;

– вектор выходных сигналов;

– вектор входных сигналов.

Каждое из матричных уравнений представляет, в сущности, систему дифференциальных уравнений, число которых для уравнения состояния равно количеству переменных состояния или порядку системы, а для уравнения наблюдения числу выходов системы.

Описание дискретных во времени систем таким методом аналогично описанию непрерывных, при этом дифференциальные уравнения заменяются разностными.