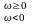- •Раздел 1: Элементы Теории Сигналов Параграф 1.1: Классификация сигналов.
- •Параграф 1.2: Пространство векторов и сигналов.
- •1.2.1: Общие сведения. Определение линейного векторного пространства.
- •1.2.2: Линейная независимость, размерность и базис линейного пространства.
- •1.2.3: Метрические и нормированные пространства. Скалярные произведения.
- •1.2.4: Функциональные пространства Евклида, Гильберта, Хемминга.
- •1.2.5: Операторы и функционалы.
- •1.2.6: Ортогональность элементов в пространстве.
- •1.2.7: Разложение сигналов в обобщенный ряд Фурье. Равенство Парсеваля
- •Параграф 1.3: Спектральное представление сигналов
- •Параграф 1.4: Тригонометрический ряд Фурье
- •Параграф 1.5: Комплексная и экспонентациальная форма представления ряда Фурье.
- •Параграф 1.6: Разложение в ряд Фурье периодическую функцию. Временное и частотное представление сигнала.
- •Параграф 1.7: Преобразования Фурье.
- •Параграф 1.8: Свойства преобразования Фурье.
- •Параграф 1.9: Сообщения, сигналы и помехи как случайные процессы. Параграф 1.9.1: Понятие случайного процесса.
- •Параграф 1.9.2: Вероятностное описание случайного процесса.
- •Параграф 1.9.3: Моментные функции случайных процессов.
- •Параграф 1.9.4: Стационарные случайные процессы.
- •Параграф 1.9.5: Эргодические случайные процессы.
- •Параграф 1.9.6: Случайные процессы, определяемые двумерной плотностью вероятности.
- •Параграф 1.9.7: Энергетический спектр случайного процесса.
- •Параграф 1.9.8: Теорема Винера - Хинчина.
- •Параграф 1.9.9: Квазибелый и белый шум.
- •Параграф 1.10: Комплексное и квазигармоническое представление сигналов. Параграф 1.10.1: Комплексное представление детерминированных сигналов.
- •Параграф 1.10.2: Комплексные случайные процессы.
- •Параграф 1.10.3: Огибающая и фаза комплексного случайного процесса. Квазигармоническое представление случайных процессов.
- •Параграф 1.10.4: Комплексная огибающая. Синфазная и квадратурная составляющая сигнала.
- •Параграф 1.10.5: Вероятностные характеристики огибающей фазы случайного процесса.
- •Раздел 2: Каналы электросвязи Параграф 2.1: Определение классификации каналов связи.
- •Параграф 2.2: Искажения и помехи в каналах связи.
- •Параграф 2.3: Математические модели каналов связи.
- •Параграф 2.3.1.: Математические модели непрерывных каналов.
- •Параграф 2.3.2: Канал с аддитивным шумом или гауссовский канал.
- •Параграф 2.3.3: Канал с неопределенной фазой сигнала.
- •Параграф 2.3.4: Канал с замиранием.
- •Параграф 2.3.5: Канал с межсимвольной интерференцией (мси) и аддитивным шумом.
- •Параграф 2.3.6: Математические модели дискретных и дискретно-непрерывных каналов.
- •Параграф 2.4: Преобразование сигналов в линейных и нелинейных звеньях каналов связи Параграф 2.4.1: Звенья каналов связи как физические системы и их математические модели. Классификация систем.
- •Параграф 2.4.2:Описание поведения линейных систем во временной области Параграф 2.4.2.1: Импульсная характеристика, интеграл Дюамеля, дифференциальные уравнения системы.
- •Параграф 2.4.2.2:Метод переменных состояний
- •Параграф 2.4.3:Описание поведения линейных систем в частной области
- •Параграф 2.4.4: Передаточная функция линейной системы
- •Параграф 2.4.5:Минимально-фазовые и неминимально-фазовые системы
- •Параграф 2.4.6.1: Основные принципы синтеза аналоговых электрических фильтров
- •Параграф 2.4.6.2: Синтез фнч
- •Параграф 2.4.6.3: Проектирование фвч и пф
- •Параграф 2.5: Нелинейные системы
- •Параграф 2.6: Параметрические системы
- •Параграф 2.7: Прохождение случайных сигналов, через линейные, параметрические и нелинейные системы Параграф 2.7.1: Прохождение случайных сигналов линейные параметрические системы. Общие сведения.
- •Параграф 2.7.2: Определение корреляционной функции отклика y4(t) линейной параметрической системы со случайной характеристикой при случайном входном воздействии
- •Параграф 2.7.3: Определение корреляционной функции отклика y3(t)
- •Параграф 2.7.4: Определение корреляционной функции отклика y2(t)
- •Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)
- •Параграф 2.7.6: Определение распределения вероятностей отклика линейной системы на случайное входное воздействие
- •Параграф 2.7.7: Прохождение случайных воздействий через нелинейные системы
- •Раздел 3: Модуляция Параграф 3.1: Общие сведения.
Параграф 1.9.8: Теорема Винера - Хинчина.
Спектральная плотность мощности можно определить по его корреляционной функции на основании следующей теоремы Минер – Хичена:
Спектральная плотность мощности стационарного случайного процесса является преобразованием Фурье от его корреляционной функции:
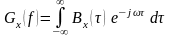
Из этой теоремы вытекает ряд следствий:
Справедливо преобразование:
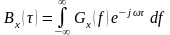 (*)
(*)Значение на нулевой частоте равно интегралу от корреляционной функции:
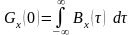
Т.к. неотрицательна, то из формулы (*) следует, что корреляционная функция случайных процессов могут быть только такие, которые имеют положительные преобразования Фурье; подобные функции называются положительно-определенными.
Формулы
для
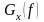 и
и
 можно записать в тригонометрической
форме, если учесть, что
так же как и
является четной функцией:
можно записать в тригонометрической
форме, если учесть, что
так же как и
является четной функцией:

Аналогичные
соотношения существуют между нормированными
функциями корреляции
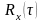 и нормированным энергетическим спектром
и нормированным энергетическим спектром
 :
:

Для одностороннего спектра:
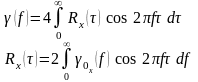
Параграф 1.9.9: Квазибелый и белый шум.
Рассмотрим
стационарный процесс
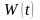 с равномерной стационарной плотностью
мощности в некоторой полосе частот.
Такой процесс называют квазибелым шумом
по его аналогии с белым светом,
представляющим собой электромагнитные
волны с равномерным спектром в области
видимых частот.
с равномерной стационарной плотностью
мощности в некоторой полосе частот.
Такой процесс называют квазибелым шумом
по его аналогии с белым светом,
представляющим собой электромагнитные
волны с равномерным спектром в области
видимых частот.
Пусть
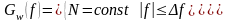

Найдем его корреляционную функцию:
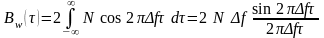
График
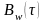 имеет вид:
имеет вид:
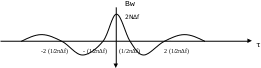
Из
графика видно, что сечения процесса
 ,
где k
– целое число, некоррелированы между
собой.
,
где k
– целое число, некоррелированы между
собой.
Если
бесконечно увеличивать
,
то придем к процессу, у которых два любых
несовпадающих сечения некоррелированы.
Такой процесс называется белым шумом.
Его спектральная плотность мощности N
постоянна на всех частотах, а коррелированная
функция
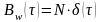 .
Изобразим его:
.
Изобразим его:

Белый шум представляет собой не реальный математический процесс, а математическую идеализацию, часто применяемую. На практике часто встречаются с процессами ……… в очень широкой полосе частот, значительно более широкой, чем полосы пропускания цепей, на которые они воздействуют, например, тепловой шум.
Из рассмотрения данного процесса видно, что увеличение интервала корреляции приводит к сокращению величины спектра и наоборот. Это является проявлением общего свойства любой пары функций, связанных между собой преобразованием Фурье.
Параграф 1.10: Комплексное и квазигармоническое представление сигналов. Параграф 1.10.1: Комплексное представление детерминированных сигналов.
В электротехнике широко используется символический метод, в соответствие с которым принято представлять гармонические колебания (ток, напряжение) в форме:
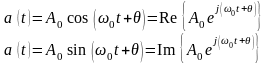
Такой прием позволяет заменить выполнение трудоемких алгебраических операций с тригонометрическими функциями более простыми действиями над комплексными величинами, облегчает решение многих задач и приводит к правильным результатам, если полученное комплексное решение заменить его действительной или мнимой частью.
В современной технике связи представление колебаний в комплексной форме получило дальнейшее развитие и распространено на негармонические сигналы. Обобщением символического метода является представление любого сложного сигнала комплексной функции:
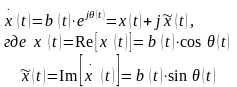
В
частном случае гармонического сигнала
 .
.
При
этом сопряженный сигнал
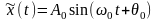 ,отличается
от действительного сигнала
,отличается
от действительного сигнала
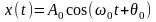 только
сдвигом фазы на (
только
сдвигом фазы на (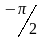 ).
).
В
общем случае негармонического сигнала
x(t) также определим сопряженный сигнал
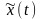 как
результат поворота фаз всех гармонических
составляющих спектральной характеристики
на (
).
Иначе говоря, если x(t) можно представить
интегралом Фурье в тригонометрической
форме:
как
результат поворота фаз всех гармонических
составляющих спектральной характеристики
на (
).
Иначе говоря, если x(t) можно представить
интегралом Фурье в тригонометрической
форме:
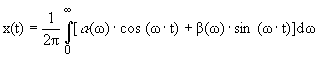
то
 ,
,
где
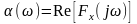 ,
,
![]()
Можно показать, что два сигнала x(t) и, удовлетворяющие этим условиям, связанны между собой во временной области интегральными преобразованиями, называемыми преобразованиями Гильберта:
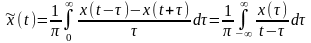
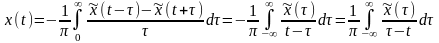
Первая из этих формул выражает прямое преобразование Гильберта, а вторая - обратное преобразование Гильберта.
Комплексный
сигнал
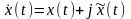 называют аналитическим сигналом, если
есть
преобразование Гильберта от
называют аналитическим сигналом, если
есть
преобразование Гильберта от
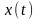 .
.
Определим,
как связан спектр аналитического сигнала
 и
спектр исходного сигнала x(t). Так как
фазы всех составляющих спектральной
плотности
и
спектр исходного сигнала x(t). Так как
фазы всех составляющих спектральной
плотности
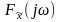 сопряженного
сигнала
в области положительных частот сдвинуты
на (
)
относительно,
сопряженного
сигнала
в области положительных частот сдвинуты
на (
)
относительно,
 ,
а умножение на j означает сдвиг фазы на
(
,
а умножение на j означает сдвиг фазы на
(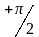 ),
то
),
то
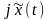 имеет
в области положительных частот такой
же спектр, как и x(t). В области же
отрицательных частот преобразование
Гильберта соответствует повороту фаз
на (
),
и поэтому спектре
фазы с отрицательными частотами сдвинуты
на
имеет
в области положительных частот такой
же спектр, как и x(t). В области же
отрицательных частот преобразование
Гильберта соответствует повороту фаз
на (
),
и поэтому спектре
фазы с отрицательными частотами сдвинуты
на
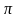 относительно спектра x(t).
относительно спектра x(t).
В результате спектр аналитического сигнала в области отрицательных частот равен нулю, а в области положительных частот спектры x(t) и складываются в одной фазе.