Параграф 1.9.7: Энергетический спектр случайного процесса.

Для описания случайных процессов наряду с корреляционными функциями широко используются спектральные характеристики, в частности, энергетический спектр (спектральная плотность мощности) . Для выяснения физического смысла этой величины проведем следующие рассуждения:

Реализация стационарного центрированного случайного процесса 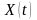в общем случае имеет бесконечную энергию, и, следовательно, не имеют преобразования Фурье.

Рассмотрим усеченный процесс 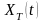, получающийся из исходного:

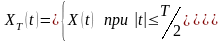
Реализация такого процесса ограничена во времени, следовательно, для них существуют преобразования Фурье.

В соответствие с равенством Парсеваля, для каждой реализации 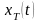этого процесса справедливо соотношение:

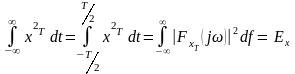
Равенство Парсеваля

где 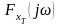– преобразование Фурье реализации ;

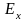– энергия сигнала.

Данное равенство показывает, что 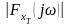характеризует распределение энергии реализации по оси частот. Усреднив эту функцию по всем реализациям процесса, получим спектральную плотность энергию процесса . Найдем математическое ожидание:

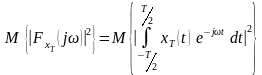
Оно определяет распределение энергии по частотам уже не одной реализации, а всего процесса . Однако с её использованием можно характеризовать лишь усеченный стационарный процесс , имеющий конечную энергию . Для того чтобы получить характеристику не усеченного стационарного процесса , обладающего бесконечной , разделим спектральную плотность энергии на Т и устремим :

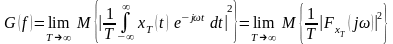
Полученная характеристика представляет собой спектральную плотность мощности стационарного процесса; определяет среднюю мощность, приходящуюся на 1 Гц на заданной частоте 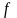. При этом, мощность обусловлена частотной составляющей в пределах очень узкой полосы 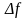вокруг средней частоты будет равна:

Поэтому эту характеристику часто называют также энергетическим спектром. Отметим некоторые свойства спектральной плотности мощности :

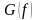1. из её определения следует, что она неотрицательна;

2. в отличие от обычной комплексной спектральной плотности, определенной преобразованием Фурье, энергетический спектр не зависит от спектра фаз реализации процесса , а однозначно определяется спектром амплитуд ;

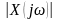3. кривая, изображающая функцию , ограничивает вместе с осью абсцисс площадь, равную мощности процесса :

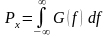
Как известно, для действительной функции модуль 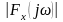является четной функцией частоты, поэтому л спектральной плотности мощности можно судить и по одной половине графика функции , например, при .

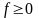В связи с этим вводят понятие односторонней спектральной плотности мощности, заданной при , таким образом:

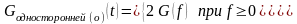
Множитель «2» в этой формуле обеспечивает равенство: 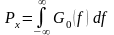. Нормированной спектральной плотностью мощности 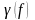или нормированным энергетическим спектром называют отношение:

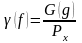
Площадь, ограничивающая 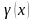и 0х, всегда равна 1.

Часто применяют математическую модель сигналов, у которых спектр отличен от 0 только в некоторой полосе частот 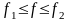, т.е. процессы с финитным спектром. Разность называют шириной спектра. В реальных условиях жесткого ограничения не бывает, и ширину энергетического спектра определяют по различным критериям. Иногда под шириной спектра понимают ширину минимальной полосы частот, в которой сосредоточена подавляющая часть (95%) мощности сигнала. Существует критерий эквивалентности прямоугольника, по которому эквивалентная ширина спектра определяется так:

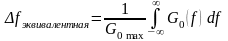
где 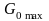– максимальное значение 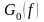в полосе частот случайного процесса.

Т.о., 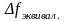– это основание прямоугольника с высотой , у которого такая же площадь, как у кривой энергетического спектра исследуемого процесса.