
- •Раздел 1: Элементы Теории Сигналов Параграф 1.1: Классификация сигналов.
- •Параграф 1.2: Пространство векторов и сигналов.
- •1.2.1: Общие сведения. Определение линейного векторного пространства.
- •1.2.2: Линейная независимость, размерность и базис линейного пространства.
- •1.2.3: Метрические и нормированные пространства. Скалярные произведения.
- •1.2.4: Функциональные пространства Евклида, Гильберта, Хемминга.
- •1.2.5: Операторы и функционалы.
- •1.2.6: Ортогональность элементов в пространстве.
- •1.2.7: Разложение сигналов в обобщенный ряд Фурье. Равенство Парсеваля
- •Параграф 1.3: Спектральное представление сигналов
- •Параграф 1.4: Тригонометрический ряд Фурье
- •Параграф 1.5: Комплексная и экспонентациальная форма представления ряда Фурье.
- •Параграф 1.6: Разложение в ряд Фурье периодическую функцию. Временное и частотное представление сигнала.
- •Параграф 1.7: Преобразования Фурье.
- •Параграф 1.8: Свойства преобразования Фурье.
- •Параграф 1.9: Сообщения, сигналы и помехи как случайные процессы. Параграф 1.9.1: Понятие случайного процесса.
- •Параграф 1.9.2: Вероятностное описание случайного процесса.
- •Параграф 1.9.3: Моментные функции случайных процессов.
- •Параграф 1.9.4: Стационарные случайные процессы.
- •Параграф 1.9.5: Эргодические случайные процессы.
- •Параграф 1.9.6: Случайные процессы, определяемые двумерной плотностью вероятности.
- •Параграф 1.9.7: Энергетический спектр случайного процесса.
- •Параграф 1.9.8: Теорема Винера - Хинчина.
- •Параграф 1.9.9: Квазибелый и белый шум.
- •Параграф 1.10: Комплексное и квазигармоническое представление сигналов. Параграф 1.10.1: Комплексное представление детерминированных сигналов.
- •Параграф 1.10.2: Комплексные случайные процессы.
- •Параграф 1.10.3: Огибающая и фаза комплексного случайного процесса. Квазигармоническое представление случайных процессов.
- •Параграф 1.10.4: Комплексная огибающая. Синфазная и квадратурная составляющая сигнала.
- •Параграф 1.10.5: Вероятностные характеристики огибающей фазы случайного процесса.
- •Раздел 2: Каналы электросвязи Параграф 2.1: Определение классификации каналов связи.
- •Параграф 2.2: Искажения и помехи в каналах связи.
- •Параграф 2.3: Математические модели каналов связи.
- •Параграф 2.3.1.: Математические модели непрерывных каналов.
- •Параграф 2.3.2: Канал с аддитивным шумом или гауссовский канал.
- •Параграф 2.3.3: Канал с неопределенной фазой сигнала.
- •Параграф 2.3.4: Канал с замиранием.
- •Параграф 2.3.5: Канал с межсимвольной интерференцией (мси) и аддитивным шумом.
- •Параграф 2.3.6: Математические модели дискретных и дискретно-непрерывных каналов.
- •Параграф 2.4: Преобразование сигналов в линейных и нелинейных звеньях каналов связи Параграф 2.4.1: Звенья каналов связи как физические системы и их математические модели. Классификация систем.
- •Параграф 2.4.2:Описание поведения линейных систем во временной области Параграф 2.4.2.1: Импульсная характеристика, интеграл Дюамеля, дифференциальные уравнения системы.
- •Параграф 2.4.2.2:Метод переменных состояний
- •Параграф 2.4.3:Описание поведения линейных систем в частной области
- •Параграф 2.4.4: Передаточная функция линейной системы
- •Параграф 2.4.5:Минимально-фазовые и неминимально-фазовые системы
- •Параграф 2.4.6.1: Основные принципы синтеза аналоговых электрических фильтров
- •Параграф 2.4.6.2: Синтез фнч
- •Параграф 2.4.6.3: Проектирование фвч и пф
- •Параграф 2.5: Нелинейные системы
- •Параграф 2.6: Параметрические системы
- •Параграф 2.7: Прохождение случайных сигналов, через линейные, параметрические и нелинейные системы Параграф 2.7.1: Прохождение случайных сигналов линейные параметрические системы. Общие сведения.
- •Параграф 2.7.2: Определение корреляционной функции отклика y4(t) линейной параметрической системы со случайной характеристикой при случайном входном воздействии
- •Параграф 2.7.3: Определение корреляционной функции отклика y3(t)
- •Параграф 2.7.4: Определение корреляционной функции отклика y2(t)
- •Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)
- •Параграф 2.7.6: Определение распределения вероятностей отклика линейной системы на случайное входное воздействие
- •Параграф 2.7.7: Прохождение случайных воздействий через нелинейные системы
- •Раздел 3: Модуляция Параграф 3.1: Общие сведения.
Раздел 1: Элементы Теории Сигналов Параграф 1.1: Классификация сигналов.
Все сигналы, используемые в технике связи и управления, можно разделить на 2 большие группы: детерминированные и случайные.
Детерминированными
сигналами
называются
сигналы, изменения которые во времени
можно предсказать заранее. Математическим
описанием (моделью) детерминированного
сигнала является строго определенная
функция х(t). Например,
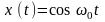 ,
где
,
где
 - известная const. При этом для любого
заданного момента ti может быть однозначно
определено значение сигнала
- известная const. При этом для любого
заданного момента ti может быть однозначно
определено значение сигнала
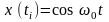 .
Случайными
сигналами
называются
сигналы, изменение которых во времени
точно предсказать его невозможно. Их
математической моделью являются
случайные функции (процессы) X (t). Они
отличаются от детерминированных сигналов
тем, что нельзя заранее утверждать, что
X (t) в конкретный момент времени ti будет
иметь какое-то определенное значение.
Можно лишь говорить о вероятности
попадания в момент t = ti значения X (ti) в
некоторый интервал
.
Случайными
сигналами
называются
сигналы, изменение которых во времени
точно предсказать его невозможно. Их
математической моделью являются
случайные функции (процессы) X (t). Они
отличаются от детерминированных сигналов
тем, что нельзя заранее утверждать, что
X (t) в конкретный момент времени ti будет
иметь какое-то определенное значение.
Можно лишь говорить о вероятности
попадания в момент t = ti значения X (ti) в
некоторый интервал
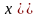 .
Если бы передаваемое сообщение было бы
детерминированным, т.е. заранее известным
с полной достоверностью, то передача
его бы не имела смысла, поскольку она
не содержит информацию. Поэтому
передаваемые полезные сообщения в ТС
так же, как и помехи, являются случайными.
Детерминированные сигналы используют
для испытания и настройки систем связи
или одно из его элементов. В зависимости
от того, какие значения могут принимать
аргумент (время t) и уровни сигналов их
делят на 4 типа:
.
Если бы передаваемое сообщение было бы
детерминированным, т.е. заранее известным
с полной достоверностью, то передача
его бы не имела смысла, поскольку она
не содержит информацию. Поэтому
передаваемые полезные сообщения в ТС
так же, как и помехи, являются случайными.
Детерминированные сигналы используют
для испытания и настройки систем связи
или одно из его элементов. В зависимости
от того, какие значения могут принимать
аргумент (время t) и уровни сигналов их
делят на 4 типа:
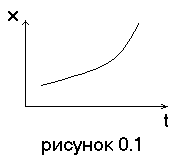
непрерывные и аналоговые сигналы. Случайные сигналы этого типа называют непрерывными случайными процессами. Они определены для всех моментов времени и могут принимать любые значения уровней из заданного диапазона. В конечном интервале времени существует бесконечное множество отсчетов непрерывного сигнала. В конечном диапазоне (Xmin – Xmax) – бесконечное множество сигналов. Чаще всего физические процессы, порожденные сигналы, являются непрерывными. Этим и объясняется второе название сигналов данного типа, т.е. аналогичные порожденных процессов.
д
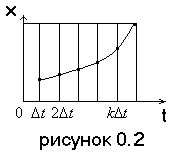 искретизированные
(дискретно-непрерывные) сигналы.
Случайные сигналы этого типа называют
процессами дискретного мира или
непрерывными случайными
последовательностями. Они определены
лишь в отдельные моменты времени и
могут принимать любые значения уровня
(непрерывные по уровню). Временной
интервал ∆t между соседними отсчетами
называется шагом дискретизации. Иногда
такие сигналы называются дискретными
по уровню.
искретизированные
(дискретно-непрерывные) сигналы.
Случайные сигналы этого типа называют
процессами дискретного мира или
непрерывными случайными
последовательностями. Они определены
лишь в отдельные моменты времени и
могут принимать любые значения уровня
(непрерывные по уровню). Временной
интервал ∆t между соседними отсчетами
называется шагом дискретизации. Иногда
такие сигналы называются дискретными
по уровню.
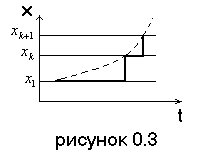
дискретные по уровню, или квантовые сигналы. Случайные сигналы этого типа называют дискретными случайными процессами. Они определены для всех моментов времени и принимают лишь разрешенные значения уровней, отделенные друг от друга на величину шага квантования ∆х.
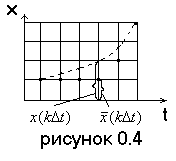
Дискретный и по уровню, и по времени сигнал. Случайные сигналы этого типа называют дискретными случайными последовательностями. Они определены лишь в отдельные моменты времени. И принимают только разрешенные значения уровня.
Сигналы, используемые в ТС, могут иметь как конечный диапазон изменения (т.е. иметь конечную длительность), так и бесконечный диапазон. Сигнал, имеющий конечную длительность, называется финитным. Сигнал, имеющий ограниченный спектр, - сигнал с финитным спектром.
