2.4. Нормированные пространства

Заметим, что эвклидова норма обладает очевидными свойствами:

1. ;

2. для любого и любого числа ;

3. для любых (неравенство треугольника).

Неотрицательность и положительная однородность функционала очевидны. Покажем неравенство треугольника:

Приняв эти свойства за аксиомы, получим следующее

Определение 1. Говорят, что на линейной структуре задана норма его элементов, если указан функционал, ставящий в соответствие этим элементам действительное число, удовлетворяющее аксиомам 1-3. Пара называется нормированным пространством.

Определение 2. Полное бесконечномерное нормированное пространство называется банаховым.

Пример. Доказать, что , где нормированное пространство,

выполняется неравенство .

.

Комментарий. 1. Ясно, что любое эвклидово пространство нормировано. Обратное, вообще говоря, неверно эвклидова норма просто одна из многих. 2. Обратим внимание, что и гильбертовы пространства как полные бесконечномерные эвклидовы пространства и банаховы пространства как полные бесконечномерные нормированные пространства построены на линейных структурах. Сейчас мы начнём строить пространства на произвольных носителях.

2.5. Метрические пространства

Комментарий. Теорию метрических пространств построил ученик Ж. Адамара, автора как термина функционал, так и термина функциональный анализ, М. Фреше. Он обобщил понятие расстояния, используемого в аналитической геометрии при изучении свойств геометрических объектов и в математическом анализе при определении предела числовой последовательности или функции.

Определение 1. Пусть – произвольное непустое множество. Говорят, что на задана метрика (расстояние) , если каждой паре элементов поставлено в соответствие единственное неотрицательное число(неотрицательный функционал) , удовлетворяющее следующим аксиомам:

1) (аксиома тождества);

2) (аксиома треугольника).

Пара , то есть множество с заданной на нем метрикой , называется метрическим пространством.

_{Комментарий.} 1.Из неравенства треугольника при сразу получаем , а при сразу получаем Но с другой стороны, неравенство треугольника можно записать так: . Тогда при сразу получаем , то есть . Тогда исходная система аксиом заменяется на часто более удобную систему из трёх аксиом:

Определение 2. Если – метрическое пространство и , то пара 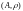также будет являться метрическим пространством и называется подпространством пространства , если , то есть расстояние между точками – равно расстоянию между этими точками в пространстве .

Комментарий. Стандартные метрические пространства – это метрические пространства со стандартными носителями и со стандартными метриками. В этих случаях пространства носят стандартные названия.

2.5.1.Стандартные носители

1. Кортежи ;

2. Ограниченные последовательности , то есть .

3. Множество непрерывных или непрерывно дифференцируемых функций на сегменте .