II. Пространства носителей

Комментарий. Главной задачей функционального анализа является изучение свойств бесконечномерных пространств и их отображений. Она возникает как естественное логическое обоснование математики в целом и математического анализа в частности. В линейной алгебре рассматриваются отображения конечномерных векторных пространств. Но во многих случаях, например при решении дифференциальных или интегральных уравнений, возникают отображения бесконечномерных векторных пространств, элементы которых представляются уже не конечными линейными комбинациями, а рядами. Поэтому центральное понятие в бесконечномерном случае сходимость последовательности элементов носителя (точек) пространства. Чтобы его ввести, нужно каким-то образом наделить пространство способом измерения расстояния между точками, а сами точки числовыми характеристиками. В конечномерных пространствах из фундаментальности последовательности следует сходимость и наоборот критерий полноты. В бесконечномерных пространствах из фундаментальности последовательности сходимость может не следовать. Поэтому полнота это ключевой атрибут пространства.

Пространство в математике это контекстно определяемое понятие.

Определение. В под пространством в функциональном анализе понимают пару 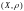, где носитель пространства, то есть некоторое множество, которое может быть как наделено определённой (например, линейной) структурой, так и нет, а заданный на элементах носителя функционал, позволяющий ввести понятие сходимости последовательности элементов носителя.

Рассмотрим стандартные пространства функционального анализа. На носителе , не наделённых линейной структурой, можно ввести метрику, свойства которой являются обобщением свойств расстояния между элементами в обычном геометрическом пространстве и построить таким образом метрические пространства. Обобщением метрических пространств являются топологические пространства. Любое метрическое пространство топологическое, обратное, вообще говоря, неверно. На носителях , наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве и построить таким образом нормированные пространства. Нормированные пространства всегда метрические и соответственно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство это нормированное пространство, где норма вводится через скалярное произведение. Иногда разделяют эвклидовы пространства на собственно эвклидовы (построенные над полем действительных чисел ) и унитарные (построенные над полем комплексных чисел ). Часто бесконечномерные эвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства это полные эвклидовы пространства. Банаховы пространства это полные нормированные пространства. То есть гильбертовы пространства это банаховы пространства, где норма вводится через скалярное произведение. Наиболее общими пространствами, фигурирующими в функциональном анализе, являются топологические пространства. Соотношения между бесконечномерными пространствами отображены на рисунке.

Этот текст в этом месте следует рассматривать как программу, потому что задачей этой главы и является определение всех этих пространств и их простейших свойств. К нему следует вернуться в конце главы.