Контрольные вопросы для самопроверки

1. Что является предметом изучения формальной логики?

2. Что такое логический закон? В чем состоит сущность этих законов?

3. Как соотносятся истинность мысли и формальная правильность рассуждений?

4. Охарактеризуйте логические постоянные, обозначающие логические операции.

Тема 2. Понятие как форма мышления Тематическое содержание

1. Понятие как форма мышления. Содержание и объем понятия.

2. Виды понятий.

3. Отношения между понятиями.

4. Операции над классами.

5. Законы логики класса.

6. Логические операции с понятиями: определение, деление, ограничение, обобщение.

Основные понятия: анализ, вычитание, деление, класс, круги Эйлера, логическая характеристика, множество, обобщение, ограничение, операции с классами, описание, определение, понятие, признак, различие, синтез, сложение, содержание, тождество, умножение, форма, характеристика.

1. Понятие – это форма мышления, отражающая предметы в их существенных признаках. Признаки предмета бывают существенными и несущественными. Для образования понятия необходимо выделить существенные признаки предмета. С этой целью применяют ряд логических приемов: сравнение, анализ, синтез, абстрагирование, обобщение.

Каждое понятие обладает содержанием и объемом. Содержанием понятия называется совокупность существенных признаков предмета, которая мыслится в данном понятии. Множество предметов, которое мыслится в понятии, называется объемом понятия. Содержание и объем понятия тесно связаны друг с другом. Эта связь выражается в законе обратного отношения между объемом и содержанием понятия, который устанавливает, что увеличение со­держания понятия ведет к образованию понятия с меньшим объемом, и наоборот.

2. Определить, к какому виду относится то или иное понятие, – значит дать ему логическую характеристику. Логическая характеристика понятий помогает уточнить их содержание и объем, вырабатывает навыки более точного употребления понятий в процессе рассуждения (рис. 1).

Виды понятий

по объему

по содержанию

собирательные

разделительные

конкретные

абстрактные

общие

единичные

нулевые

положительные

отрицательные

относительные

безотносительные

регистрирующие

нерегистрирующие

Рис. 1

По объему понятия делятся на единичные, общие и нулевые (пустые). Единичные – это такие понятия, объем которых составляет один элемент. Общими называются такие понятия, объем которых составляет два и более элемента. Нулевые понятия – это понятия, объемы которых отражают пустые предметные области, им не соответствуют никакие реальные объекты; предметная область которых равна нулю.

Общие понятия делятся на регистрирующие и нерегистрирующие. Регистрирующие – это такие понятия, объем которых составляет конечное множество элементов, в принципе поддающихся учету. Нерегистрирующие – такие понятия, объем которых составляет бесконечное множество элементов и не поддается принципиальному учету.

По содержанию понятия делятся на конкретные и абстрактные. Конкретными называются понятия, в которых мыслятся предметы в совокупности своих признаков. Абстрактными называются понятия, в которых мыслятся свойства или отношения, отвлеченные от самих предметов.

Понятия делятся также на собирательные и разделительные. Разделительные – такие понятия, в объеме которых каждый индивидуальный предмет мыслится как элемент класса. Собирательные – такие понятия, в которых предметы мыслятся как единое целое.

Понятия бывают положительные и отрицательные. Положительными называются понятия, которые выражают наличие у предмета определенных признаков. Отрицательными называются такие понятия, в которых выражается отсутствие признака, зафиксированного в положительном понятии.

По содержанию понятия делятся на соотносительные и безотносительные. Соотносительные – такие понятия, в которых выражаются предметы, существование одного из которых немыслимо без существования другого. Безотносительные – такие понятия, в которых отражаются предметы, существование которых не связывается необходимым образом с существованием других предметов.

3. Рассматривая отношения между понятиями, следует, прежде всего, различать понятия сравнимые и несравнимые. Сравнимыми называются понятия, имеющие некоторые признаки, позволяющие эти понятия сравнивать друг с другом. Несравнимыми называются понятия, не имеющие общих признаков, поэтому и сравнивать эти понятия невозможно. Сравнимые понятия делятся на совместимые и несовместимые.

Выделяют три вида отношений совместимости:

• равнообъемность – понятия, в которых мыслится один и тот же предмет, объемы их полностью совпадают;

• пересечение – понятия, объем одного из которых частично входит в объем другого;

• подчинение – понятия, объем одного из которых полностью входит в объем другого, составляя его часть.

Несовместимые – понятия, объемы которых не совпадают ни полностью, ни частично. Отношения несовместимости:

• соподчинение – два или больше неперекрещивающихся понятий, подчиненных общему для них понятию;

• противоположность – понятия, одно из которых содержит некоторые признаки, а другое – признаки, не совместимые с ними;

• противоречие – понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.

4. При помощи логических операций из двух или нескольких клас­сов могут быть образованы новые классы. Класс – это совокупность объектов, которые имеют один или несколько общих признаков. К операциям с классами отно­сят:

• сложение классов (А 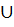B) – это логическая операция, в результате которой из двух или более классов образуется новый класс, состоящий только из тех элементов, каждый из которых является элементом хотя бы одного входящего класса;

• умножение классов (A 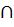B) – это логическая операция, в результате которой образуется новый класс тех и только тех элементов, которые являются общими для пересекающихся классов;

• вычитание классов – это логическая операция в результате которой получается класс, состоящий из элементов, исключающих элементы вычитаемых классов;

• образование дополнения к классу. Отношения между дополняемым классом и его дополнением есть отношения противоречия, которое характеризуется тем, что каждый из объектов какой-нибудь универсальной области может мыслиться в объеме только одного из противоречащих понятий. Из этого свойства противоречащих понятий вытекают все законы операции дополнения.

5. Выделяют следующие законы логики классов:

1) Закон идемпотентности – класс, сложенный самим собой, помноженный на самого себя, равен самому себе:

А ∪ А = А;

А ∩ А = А.

2) Закон коммутативности – сумма двух классов, а также их произведение не зависят от порядка выполнения действия:

А ∪ В = В ∪ А;

А ∩ В = В ∩ А.

3) Закон ассоциативности – сумма более чем двух классов, а также их произведение не зависят от порядка выполнения действия:

А ∪ (В ∪ С) = (А ∪ В)∪ С;

А ∩(В ∩ С) = (А ∩ В) ∩ С.

4) Закон поглощения (элиминации).

• Элиминация сложения относительно умножения:

А ∪(А ∩ В) = А – сумма некоторого класса и произведение двух классов, одним из множителей которого является данный класс, равна ему самому.

• Элиминация для умножения относительно сложения:

А ∩(А ∪ В) = А – произведение некоторого класса и суммы двух классов, одним из слагаемых которого является данный класс, равна ему самому.

5) Закон дистрибутивности.

• Дистрибутивность умножения относительно сложения:

А ∩ (В ∪ С) = (А ∩ В) ∪ (А ∩ С).

• Дистрибутивность сложения относительно умножения:

А ∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С).

6) Законы дополнения.

• Сумма дополнения и дополняемого класса равна универсальному классу: А¹ ∪ А = 1.

• Произведение дополнения и дополняемого класса равно пустому множеству или нулю: А¹ ∩ А = 0.

• Сумма дополняемого класса и универсального множества равна универсальному множеству: А ∪ 1 = 1.

• Произведение дополняемого класса и универсума равно дополняемому классу: А ∩ 1 = А.

• Дополнение пустого класса равно универсальному множеству: 0¹ = 1.

• Дополнение универсального класса равно универсальному классу: 1¹ = 0.

6. Определение понятия – это логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина.

Логическая операция, раскрывающая объем понятия, называется делением. Сущность деления состоит в том, что предметы, входящие в объем делимого понятия, распределяются по группам. Различают деление 1) по видоизменению признака и 2) дихотомическое деление.

Обобщить понятие – это значит осуществить логическую операцию перехода от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Ограничить понятие – значит перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но большим содержанием. Обобщение и ограничение понятий не следует смешивать с мысленным переходом от части к целому и выделением части из целого.

Все операции с понятиями имеют правила, которые необходимо соблюдать, чтобы результат операций получился правильным.