10 Вопрос

Циркуляция векторного поля

Циркуля́цией ве́кторного по́ля по данному замкнутому контуру Γ называется криволинейный интеграл второго рода, взятый по Γ. По определению

где   — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,   — бесконечно малое приращение радиус-вектора   вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.

Свойства циркуляции

Свойство аддитивности циркуляции: циркуляция по контуру  есть сумма циркуляций по контурам   и  , то есть 

Аддитивность

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

Формула Стокса

Циркуляция вектора F по произвольному контуру Г равнапотоку вектора   через произвольную поверхность S, ограниченную данным контуром.

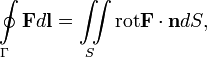
где 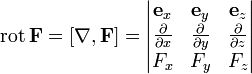  — ротор (вихрь) вектора F.

В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина

где   — плоскость, ограничиваемая контуром  (внутренность контура).

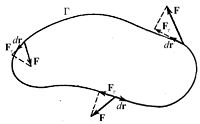
Физическая интерпретация

Физическая интерпретация циркуляции: Работа поля по замкнутому контуру

Если F — некотороесиловое поле, тогда циркуляция этого поля по некоторому произвольному контуру Γесть работа этого поля при перемещении точки вдоль контура Г. Отсюда непосредственно следует критерийпотенциальности поля: поле является потенциальным когда циркуляция его по произвольному замкнутому контуру есть нуль. Или же, как следует из формулы Стокса, в любой точке области D ротор этого поля есть нуль.

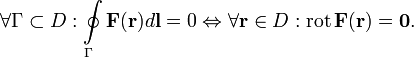
11 Вопрос

Условие потенциальности векторного поля

Потенциальное поле.

 Рассмотрим некоторое скалярное поле F(М}. Если в каждой точке М из G определен вектор grad F, то поле этого вектора наз потенциальным полем. Само скалярное поле называется при этом потенциалом векторного поля, а вектор, определяющий потенци­альное поле, часто наз потенциальным вектором, т. е. век­тор а(М) потенциальный, если найдется такая скалярная функция F{М). Что a= grad F=∂F/∂x*I+∂F/∂y*j+∂F/∂z*r.—1--

Возникает вопрос, при каких условиях данное векторное поле а{М} потенциальное. Пусть Р,Q и R -проекции вектора а на оси координат Оx, Оу, Оz соответственно, т. е. a=a(M)=Pi+Qj+Rr.В силу соотношения (1) векторное поле a(М) является потенци­альным, если найдется функция F(М) такая, что ∂F/∂x=P, ∂F/∂y=Q, ∂F/∂z=R—2--

Выражение Pdx+Qdy+Rdz полный дифферен­циал некоторой функции Р(х, у, z} в том и только в том случае,когда Р,Q,Rудовлетворяют условиям ∂P/∂y=∂Q/∂x; ∂Q/∂z=∂R/∂y; ∂R/∂x=∂P/∂z—3--

Но если Pdx+Qdy+Rdz=dF, то справедливы и равенства (2), т. е. условие (3) как раз и означает, что данное векторное поле потенциальное. Функция F(х,у,z) в этом случае называется по­тенциальной функцией поля.

Примером потенциального поля служит поле сил тяготения.

Скалярный потенциал

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см.Потенциал.

Скалярный потенциал векторного поля   (чаще простопотенциал векторного поля) — это скалярная функция  такая, что во всех точках области определения поля

где   обозначает градиент  . В физике обычно потенциалом называют величину, противоположную по знаку (потенциал силы, потенциал электрического поля).

Потенциальные поля[править | править исходный текст]

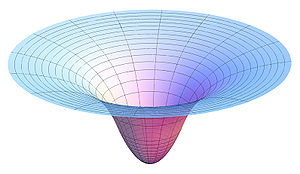
График гравитационного потенциала однородного диска в его плоскости.

Поле называется потенциальным, если для него существует скалярный потенциал. Для потенциального полякриволинейный интеграл между двумя точками

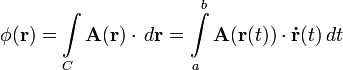
не зависит от пути интегрирования  , соединяющего эти точки. Это равносильно тому, что интеграл по любому замкнутому контуру   равен нулю:

Непрерывное векторное поле в односвязной областитрёхмерного пространства потенциально тогда и только тогда, когда оно безвихревое:

Обобщением этой теоремы на случай произвольного конечномерного пространства является лемма Пуанкаре. Для таких пространств существует изоморфизм между векторными полями   и 1-формами  , при этом вопрос о существовании потенциала сводится к вопросу об обращениивнешнего дифференцирования. Лемма Пуанкаре утверждает, что любая замкнутая форма в односвязной области конечномерного пространства точна.

Заметим, что в общем случае неодносвязного пространства условия замкнутости недостаточно. Легко проверить, что поле на плоскости

является безвихревым в любой односвязной области, не содержащей точку  , однако

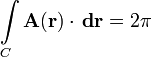
для любого контура  , один раз обходящего вокруг начала координат против часовой стрелки.

Опера́тор на́бла (оператор Гамильтона) — векторныйдифференциальный оператор, обозначаемый символом  (набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах^[1]оператор набла определяется следующим образом:

,

где   — единичные векторы по осям x, y, zсоответственно.

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div(дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ  используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор с компонентами   в n-мерном пространстве^[2].

Иногда, особенно при начертании от руки, над оператором набла рисуют стрелку:   — чтобы подчеркнуть векторный характер оператора. Смысл такого начертания ничем не отличается от обычного  .

• Иногда (особенно когда речь идет только о применении к скалярным функциям), оператор набла называютоператором градиента, каковым он в применении к скалярным функциям (полям) и является.

• Замечание: в физике в наше время название оператор Гамильтона по отношению к оператору набла стараются не употреблять, особенно в квантовой физике, во избежание путаницы с квантовым гамильтонианом, имеющим, в отличие от классического, операторную природу.

• Опера́тор Лапла́са (лапласиа́н, оператор дельта) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом  . Функции 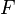  он ставит в соответствие функцию  .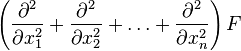

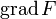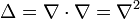• Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции:  , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков)потенциального векторного поля   в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.