2 Вопрос.

Двойной интеграл в полярных координатах

Пусть область D записывается системой неравенств в полярных координатах:

Такая область называется правильной в полярной системе координат, если каждый луч, выходящий из полюса, пересекает границу области не более, чем в 2-x точках.

 

По определению   .

Т. к. значение двойного интеграла не зависит от способа разбиения области D на элементарные части, то сделаем это разбиение координатными линиями полярной системы координат (лучами из полюса и концентрическими окружностями).

Переведенный в полярные координаты двойной интеграл сведен к повторному по имеющейся записи области D неравенствами для переменных   и   . В результате получаем формулу для вычисления двойного интеграла в полярных координатах:

 .

Обратите внимание, что в правой части формулы присутствует множитель   - это якобиан (определитель Якоби) преобразования, который находится следующим образом:

Вычисление двойного интеграла в декартовых координатах

О: Область D называется правильной в направлении оси OY (ОХ), если любая прямая, параллельная оси OY(OX) и проходящая через внутреннюю точку области Д пересекает ее границу в двух точках.

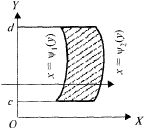
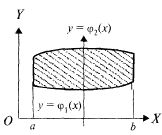
Рис. 23.3

Рис. 23.4

Граница области D, правильной в направлении оси OY (рис. 23.3), может быть задана уравнениями

 и двойной интеграл в этом случае вычисляется по формуле

 (23.5)

причем сначала вычисляется внутренний интеграл

в котором х считается постоянной. Выражение справа в (23.5) называется повторным, или двукратным интегралом.

Граница области D, правильной в направлении оси ОХ (рис. 23.4), может быть задана уравнениями:

 Тогда двойной интеграл вычисляется по формуле

 (23.6)

Если область D правильная в направлении ОХ и OY (правильная область), то применимы обе формулы.

Рассмотрим геометрический смысл формулы (23.5), для формулы (23.6) рассуждения аналогичные (вывод формул приведен в [6. С. 310]).

Предположим, что и граница области D является правильной в направлении оси OY.

Из разд. 23.1

Подсчитаем теперь объем V методом поперечных сечений (см. п.18.2.1):

 (23.7)

Проводя через т. (х,0,0) плоскость перпендикулярно оси ОХ, получим в сечении криволинейную трапецию

(рис. 23.5), с площадью

для точек линии при постоянном х зависит только от у:

 - (23.8)

площадь поперечного сечения цилиндрического тела. Подставляя (23.8) в (23.7), получаем

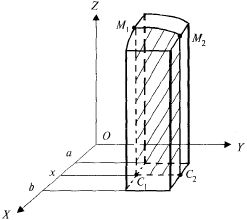
Рис. 23.5

Таким образом, в формуле (23.7) слева и справа имеем объем цилиндрического тела.

Формулы (23.5) и (23.6) выведены в предположении, что область имеет специальный вид.

В общем случае область D разбивают на конечное число частей, являющихся правильными, и вычисляют для каждой из частей интеграл по формуле (23.5) или (23.6). Интеграл по всей области (свойство 3°) равен сумме полученных интегралов.

Если область ГУ. то формулы (23.5) и (23.6)

примут вид

3 Вопрос.

Задача о вычислении массы неоднородного тела T по известной объемной плотности ρ(M) этого тела естественным образом приводит нас к понятию тройного интеграла.

     Для вычисления массы указанного тела T разобьем его на достаточно малые участки T₁, T₂, ..., T_n. Приближенно можно считать объемную плотность ρ(M) каждого участка T_k постоянной и равной ρ(M_k), где M_k - некоторая точка участка T_k. В таком случае масса каждого участка T_k будет приближенно равна ρ(M_k) · v_k, где v_k - объем участка T_k.

     Приближенное значение массы всего тела T будет равно сумме

Точное значение массы естественно определить как предел указанной суммы при неограниченном уменьшении каждого участка T_k. Этот предел и может быть взят за определение тройного интеграла от функции ρ(M_k) по трехмерной области T.