2. Необходимый признак сходимости.

Теорема.

Если числовой ряд   сходится, то его общий член при неограниченном возрастании n стремится к нулю, т.е.

Доказательство.

Пусть данный ряд сходится. Тогда по определению сходящегося ряда

;

так как вместе с   также и  , то  , т.е.

Здесь  , а  .

Поэтому 

Отсюда  , что и требовалось доказать.

Теорема 4 (необходимый признак сходимости). Если ряд   сходится, то  .

Доказательство. Так как ряд сходится, то частичная сумма S_n (а с ней и S_n–1) имеет конечный предел  . Но

,

отсюда  .

Замечание. Следует заметить, что это только необходимый признак сходимости, но недостаточный, т. е. обратное утверждение неверно, и, если  , о сходимости ряда ещё ничего нельзя сказать. Но если  , то ряд расходится, что является достаточным условием расходимости.

29 Вопрос

Теорема сравнения рядов с положительными членами

Пусть даны два числовых ряда с положительными членами:

 (1) и

 (2),

Тогда имеет место следующая теорема.

Теорема.

Если члены ряда (1) не больше соответствующих членов ряда (2), т.е.

 (3)

И ряд (2) сходится, то сходится и ряд (1), а если ряд (1) расходится, то и ряд (2) тоже расходится.

Доказательство.

1) обозначим через   и   частичные суммы рядов (1) и (2) соответственно. Из условия (3) следует, что

 (4)

Так как ряд (2) сходится, то существует  , а из того, что члены рядов (1) и (2) положительны, следует, что   и тогда в силу неравенства (4)  .

Мы доказали, что частичные суммы   ограничены, а так как последовательность частичных сумм является ещё и возрастающей, то она имеет предел  , причем, очевидно, что

2)Докажем теперь, что из расходимости ряда (1) следует расходимость ряда (2). Предположим, что ряд (2) сходится, но тогда по только что доказанной теореме сходился бы и ряд (1), что противоречит условию теоремы.

Исследуем ряды на сходимость с помощью признака сравнения.

Вторая (предельная) теорема сравнения

Постановка задачи. Исследовать сходимость ряда с положительными членами

.

План решения.

1. Проверяем, что  , т.к. если  , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Проверяем, что   для всех  .

3. Делаем вывод о сходимости или расходимости ряда, используя вторую (предельную) теорему сравнения:

Пусть даны два ряда   и  , причем существует номер   такой, что при всех     и  . Если существует конечный и отличный от нуля предел

,

то ряды   и   либо оба сходятся, либо оба расходятся одновременно.

В качестве эталонного ряда   обычно используют либо обобщенный гармонический ряд  , который сходится при   и расходится при  , либо геометрический ряд  , который сходится при   и расходится при  . Таким образом, необходимо найти последовательность   (или  ) такую, что

 (или  ) при  .

Вывод: по второй (предельной) теореме сравнения исходный ряд   сходится, если   ( ) и расходится, если   ( ).

30 Вопрос

Признак Даламбера.

Теорема 7: Пусть дан ряд с положительными членами и существует предел . Тогда а) при ряд сходится; b) при ряд расходится.

Доказательство.

a) Пусть и . Докажем, что ряд сходится. По определению предела числовой последовательности для любого существует номер N такой, что при выполняется неравенство . Отсюда следует, что . (8)

Т.к. , то можно взять настолько малым, что будет выполнено неравенство . Полагая , на основании правого из неравенств (8) имеем , или для n=N, N+1, N+2, … Придавая n эти значения, из последнего неравенства получаем

т.е. члены ряда (9)

меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии:

(10)

Т.к. , то ряд (10) сходится. Тогда согласно признаку сравнения ряд (9) также сходится. Но ряд (9) получен из данного ряда в результате отбрасывания конечного числа первых членов, следовательно, по теореме 1 ряд сходится.

b) Пусть теперь . Докажем, что ряд расходится. Возьмем настолько малым, чтобы . Тогда при в силу левого из неравенств (8) выполняется неравенство или . Таким образом, члены ряда, начиная с некоторого номера N, возрастают с увеличением их номеров, т.е. общий член ряда не стремится к нулю при . Следовательно, согласно теореме 4, ряд расходится.

Замечание. При ряд может, как сходится, так и расходится. В этом случае необходимо дополнительное исследование ряда с помощью признака сравнения или других признаков.

Теорема Коши

Если для числового ряда

с неотрицательными членами существует такое число , , что, начиная с некоторого номера, выполняется неравенство , то данный ряд сходится

Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда , то если ряд сходится, если ряд расходится, если 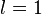вопрос о сходимости ряда остается открытым.

Теорема Маклорена-Коши

Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на , последний часто может быть найден в явном виде.

Пусть для функции f(x) выполняется:

1. (функция принимает неотрицательные значения)

2. (функция монотонно убывает)

3. (соответствие функции ряду)

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Обобщенный гармонический ряд

Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд^[3]

.

Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1^[3].

Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:

Для чётных это значение явно выражается через число пи, например, , а уже для α=3 его значение аналитически неизвестно.