18. Метод зон Френеля. Дифракция Френеля на круглом отверстии и диске.

1. Пусть источник света S₀ испускает сферическую волну. Поставим на пути волны непрозрачный экран Э₁ с круг­лым отверстием АВ таким об­разом, чтобы перпендикуляр, опущенный из S₀ на экран, проходил через центр отвер­стия (рис. 3.4 а). Для наблюде­ния дифракционной картины параллельно Э₁ на расстоянии L от него поместим экран Э₂. Ис­пользуя метод зон Френеля, разобьем открытую часть волнового фронта АВ на зоны и определим результирующую амплитуду светового вектора в точке Р. Число открытых зон Френеля m за­висит от размеров отверстия АВ, расстояния Lи длины волны света λ. Если m – нечетное число, суммарная амплитуда в точке Р будет равна Е₁/2 + Е_m/2, что соответствует интерференцион­ному максимуму На рис. 3.4 б показано, как меняется интен­сивность света на экране Э₂ в зависимости от расстояния r от центра экрана P. Следовательно, наличие преграды с круглым отверстием усиливает освещенность в точке Р, т.к. без экрана амплитуда в данной точке была бы равна Е₁/2. Если m – четное число, результирующая амплитуда в точке Р:

.

Поскольку амплитуды двух соседних зон Френеля мало отличаются друг от друга, можно предположить, что   и тогда результирующая амплитуда запишется в виде:   и в точке Р будет наблюдаться интерференционный минимум (рис. 3.4 в). Чтобы найти результирующую амплитуду в другой точке экрана, например, Р’, необходимо разбить фронт волны на зоны с центром в точке О’ (рис. 3.4. а). В этом случае часть первоначальных зон будет закрыта экраном Э₁. Амплитуда в точке Р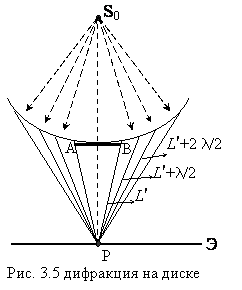 ’ будет определяться не только числом зон, уклады­вающихся на отверстии, но и степенью частичного перекрыва­ния зон. Исходя из соображений симметрии, дифракционная картина должна состоять из чередующихся светлых и темных колец, что и было подтверждено экспериментально. По мере удаления от центра экрана интенсивность максимумов убывает. ЕслиS₀ – источник белого света, светлые кольца имеют радуж­ную окраску.

2. Пусть между источником света S₀ и экраном Э разме­щен непрозрачный диск АВ, параллельный экрану (рис. 3.5). Пунктирная прямая S₀Р перпендикулярна диску и проходит че­рез его центр. Вновь воспользуемся методом зон Френеля. Пусть диск закрывает m зон, тогда амплитуда первой действующей зоны будет Е_m+1. С нее и следует начинать построение зон. В ре­зультате суммирования ам­плитуд всех открытых зон мы получаем, что в точке Р амплитуда Е = Е_m+1/2. Таким образом, при дифракции на круглом не­прозрачном диске в центре экрана получается светлое пятно (т.к. интенсив­ность здесь отлична от нуля), ок­руженное чередующимися концентрическими коль­цами минимумов и макси­мумов.

 

19. Дифракция Фраунгофера на прямоугольной щели.

Дифракцию в парал­лельных лучах или дифракцию плоских волн впервые иссле­довал немецкий физик И. Фра­унгофер в 1821-1822гг. Пусть плоская монохроматическая волна падает нормально на не­прозрачный экран Э₁ с длинной узкой щелью АВ шириной а (рис. 3.6). Согласно принципу Гюйгенса – Френеля все точки щели можно рассматривать как вторичные источники световых волн, колеблющихся в одной фазе (так как плоскость щели есть часть волновой поверхности падающей плоской волны), и распространяющихся во всех направлениях. Из всего многооб­разия направлений выберем одно произвольное и будем рас­сматривать лучи, идущие под углом φ к падающим лучам. Па­раллельно экрану Э₁поместим линзу Л, а в ее фокальной плос­кости – экран Э₂, на котором лучи соберутся в некоторой точке Р. Опустим перпендикуляр АС из точки А на крайний луч. АС представляет собой волновую поверхность для лучей, идущих под углом φ и, согласно определению, все точки данной поверх­ности колеблются в одной фазе. Поэтому отрезок ВС является оптической разностью хода между крайними лучами пучка, ВС = Δ = аsinφ. Поделим участок ВС на отрезки, равные λ/2 и из то­чек деления проведем плоскости, параллельные АС до пересе­чения с АВ (эти плоскости перпендикулярны рисунку и поэтому на нем изображены как прямые линии). Эти плоскости поделят щель АВ на равные полоски, которые являются зонами Френеля, т.к. световые волны, идущие от соседних полосок, имеют раз­ность хода λ/2 (см. рис. 3.6). Если число зон будет четным, они попарно погасят друг друга, и в точке Р будет наблюдаться ми­нимум освещенности. Четное число отрезков на участке ВС со­ответствует условию аsinφ = ±2m λ/2, где m = 1,2,3…Это усло­вие называется условием дифракционного минимума. Из него находятся углы, под которыми наблюдаются дифракционные минимумы на экране. Знак “минус” соответствует лучам, иду­щим от щели под углом –φ.

Если число зон Френеля нечетно, на экране в точке Р по­лучается дифракционный максимум. Условие дифракционного максимума имеет вид

аsinφ = ±(2m + 1)λ/2, где m = 1, 2, 3…

Это условие определяет углы, соответствующие макси­мумам освещенности на экране Э₂. Число m называется поряд­ком дифракционного максимума или минимума.

В центральной точке экрана О соберутся лучи, идущие в направлении φ = 0, следовательно, без разности хода. В этом на­правлении щель действует как одна зона Френеля, создавая в точке О самый интенсивный максимум нулевого порядка. Это будет светлая полоса, повторяющая форму щели. Дифракцион­ная картина от щели симметрична относительно точки О и ин­тенсивности максимумов более высоких порядков уменьшаются в пропорции 1 : 0,047 : 0,017 : 0,008…

Дифракционная картина на экране зависит от отношения длины волны падающего монохроматического излучения λ к ширине щели а. Из условия дифракционного минимума  , следовательно расстояния от центра картины до мини­мумов возрастают с уменьшением а. Центральная светлая полоса при этом расширяется. При а«λ вся поверхность щели будет небольшой частью лишь одной зоны Френеля. Такую щель можно считать линейным источником света, колебания от которого будут распространяться в одной фазе и дифракцион­ной картины не наблюдается. При а»λ в центре экрана получа­ется широкая равномерно освещенная полоса, обусловленная беспрепятственным прямолинейным распространением света от источника, и на ее краях наблюдаются очень узкие дифракцион­ные полосы.

При освещении щели белым светом дифракционные мак­симумы, соответствующие различным длинам волн пространст­венно разделятся. Чем меньше длина волны, тем ближе к центру экрана будет располагаться ее максимум. Это следует из усло­вия максимума при дифракции от одной щели. В центре экрана объединятся лучи всех длин волн, так как здесь угол φ = 0 и раз­ность хода Δ = 0, поэтому центральный максимум будет белым. Максимумы первого, второго и высших порядков разложатся в спектры, обращенные фиолетовым краем к центру экрана. По­добные спектры расплывчаты, поэтому четкое разделение по длинам волн при дифракции от одной щели получить не уда­ется. Для получения более качественной дифракционной кар­тины свет от источника необходимо пропустить через несколько параллельных щелей.