1. Дифференциальное уравнение Свободные НЕзатухающие колебания в электрическом колебательном контуре.

Классифицируя колебания, их делят, прежде всего, на собственные и вынужденные. Представить себе собственные колебания осциллятора очень просто: отведите из положения равновесия обычный маятник и отпустите. Движение, которое за этим последует, и есть собственные колебания маятника.

Если же колебания поддерживаются периодической «вынуждающей» силой, то возникнут вынужденные колебания.

Мы обращаемся к рассмотрению собственных колебаний, амплитуда которых не меняется во времени. Такие колебания называются собственными незатухающими.

Это дифференциальное уравнение собственных незатухающих колебаний пружинного осциллятора. Его принято записывать так:

(12.3)

Решением этого уравнения является гармоническая функция

x = a Cos (w₀t + a).

2.Дифференциальное уравнение Свободные затухающие колебания в электрическом колебательном контуре.

Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R≠0) , как известно    Учитывая формулу собственной частоты колебательного контура и принимая коэффициент затухания равным   (11)  дифференциальное уравнение колебаний заряда Q (см. раздел "Свободные гармонические колебания в колебательном контуре") можно записать в аналогичном уравнению (1) виде    Из зависимостей (1) и (5) следует, что колебания заряда подчиняются закону   (12)  с частотой, используя (4), равной   (13)  меньшей собственной частоты контура ω₀ . При R=0 формула (13) становится формулой (4).  Логарифмческий декремент затухания задается формулой (7), а добротность колебательного контура (8)   (14)  Отметим в заключение, что при увеличении коэффициента затухания δ период затухающих колебании увеличивается и при δ=ω₀равен бесконечности, т. е. движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически стремится к нулю, когда t→∞. Данный процесс не будет колебательным. Он называется апериодическим.  Значительный интерес для техники представляет возможность сохранять колебания незатухающими. Для этого необходимо восполнять каким-либо образом потери энергии реальной колебательной системы. Особенно важны и широко используются так называемые автоколебания — незатухающие колебания, которые поддерживаются в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний задаются самой системой.  Автоколебания принципиально отличаются от свободных незатухающих колебаний, которые происходят без действия сил, а также от вынужденных колебаний (см. следующий раздел), которые происходят под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).  Примером автоколебательной системы являются часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, которая передавается при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также появляются вследствие автоколебаний, поддерживаемых воздушной струёй.  3. Коэффициент затухания, логарифмический декремент затухания, добротность.

Скорость затухания колебаний определяется коэффициентом затухания . В соответствии с выражением коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда колебаний уменьшается в «e»=2.718 раз. Период затухающих колебаний определяется формулой:

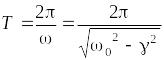
При незначительном затухании ( ) период колебаний практически равен 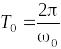. С ростом период увеличивается. Из соотношения следует, что .

Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

.

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз. Помимо рассмотренных величин для характеристики колебательной системы употребляется величина , называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз. Большим значениям добротности соответствует малое затухание.

4. Дифференциальное уравнение вынужденных электромагнитных колебаний. Резонанс

Если рассматривать колебательный контур, то для получения вынужденных колебаний (рис. 8.4), нужно включить последовательно с элементами контура переменную эдс или, разорвав контур, подать напряжение:

Рис. 8.4. Вынужденные колебания в колебательном контуре

U = U_mcosw, тогда уравнение будет иметь вид:

  ,                                                                                                           (8.15)

 

после замены получим

  .                                                                                     (8.16)

 

Резонансная частота для контура

  .                                                                        

При   резонансные кривые стремятся к U_m – напряжению, возникающему на конденсаторе при подключению его к источнику постоянного напряжения. Максимум при резонансе получается тем выше и острее, чем меньше  , т. е. чем меньше активное сопротивление и больше индуктивность контура. Тогда амплитуда силы тока имеет максимальное значение при  . Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура  .

5. Первое уравнение Максвела

Первое уравнение Максвелла –есть обобщенное уравнение Ампера и Био, Савара на токи смещения.

В современной интегральной форме это уравнение имеет вид:

                                                                         =                                                               

Где 

                                                                                                                                                       

 

Уравнение 1.1 означает, что круговые магнитные поля создаются как токами проводимости так и токами смещения.

Полный ток   является замкнутым.

Подставим 1.2 в 1.1 получим:

                                                            ;                                                       

Получим дифференциальную форму 1-го уравнения Максвела.                                                                         ;                                                             

                                                                        rot ;                                                                       

1-е уравнение Максвела в дифференциальной форме говорит о том, что вихревое магнитное поле создается как токами смещения, так токами проводимости.

Уравнения Максвела в дифференциальной форме не справедливо в средах, где имеется скачек эл-х характеристик среды. Но интегральное уравнение справедливо и для этих сред.

6. Второе уравнение Максвела

Второе уравнение Максвела - есть обобщение закона Фарадея на диэлектрические среды.

                                                                                                                                          

-2-е уравнение Максвела в интегральной форме.

Получим дифференциальную форму этого уравнения

                                                                                                                                   

Это уравнение справедливо, если равны подинтегральные выражения

                                                                      rot                                                                        

2-е уравнение Максвела означает, что переменное во времени магнитное поле вихревое электрическое поле в пространстве.

Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения   (с точностью до универсального постоянного коэффициента) называется^[3] поток вектора быстроты изменения электрического поля   через некоторую поверхность^[4]  :

 (СИ)

 (СГС)

В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:

 (СИ)

 (СГС),

где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)