14. Производство и производственная функция. Изокванты и их свойства

Сущность производственной функции

Технологическая зависимость между количеством ресурсов, затрачиваемых фирмой в единицу времени, и максимально возможным объемом выпускаемой продукции называют производственной функцией.

В наиболее общем виде производственная функция может быть записана в виде

Q = f(X1,X2,...Xn),

где Q - объем выпуска в единицу времени,

X1,X2,...Xn - количество используемых ресурсов в единицу времени.

Производственная функция характеризует техническую зависимость между ресурсами и выпуском и описывает всю совокупность технологически эффективных способов производства. Каждый способ производства (технология) может быть описан своей производственной функцией. И соответственно, изменение технологии производства влечет за собой изменение и самой функции.

Важно отметить, что производство, не обеспечивающее максимально возможный объем выпуска при данном объеме ресурсов, считается неэффективным и, согласно одному из исходных принципов микроэкономики (принципу рациональности), не используется рациональным предпринимателем.

Подобно любой другой функции, производственная функция может быть записана в виде таблицы, уравнения или представлена графиком.

В микроэкономике используется большое количество самых разнообразных функций производства, но чаще всего - двухфакторные функции вида

Q = f(X;Y),

которые легче анализировать в силу возможности их графического представления.

Среди двухфакторных функций наибольшую известность получила функция Кобба-Дугласа, имеющая вид:

,

где а,  - положительные константы;

X, Y - количество используемых ресурсов (обычно рассматривают труд и капитал).

Зная свою производственную функцию, фирма может оценить, как изменится объем ее выпуска, если она увеличит или уменьшит количество одного из используемых ресурсов, оставив неизменными все прочие ресурсы, или увеличит количество всех используемых ресурсов в равной или неравной мере.

Краткосрочная функция производства

Деятельность фирмы в краткосрочном периоде может быть охарактеризована при помощи краткосрочной функции производства, предполагающей наличие у фирмы частично постоянных и частично переменных ресурсов.

Q = f( ,L),

где К - количество постоянного ресурса;

L - количество переменного ресурса.

Краткосрочная функция производства показывает максимальный объем выпуска, который фирма может произвести, изменяя количество и комбинацию переменных ресурсов, при данном количестве постоянных ресурсов.

Для упрощения нашего анализа предположим, что фирма использует всего два ресурса: переменный ресурс - труд (L) и постоянный ресурс - капитал (К).

Рисунок 5.1 – Графическое изображение совокупного, среднего и предельного продуктов

Графическое изображение функции производства

Представим графически полученные нами результаты. Как видно из рис. 5.1, функция производства в своем развитии проходит три этапа.

На первом этапе (при L от 0 до L3) происходит повышение отдачи переменного ресурса (т. е. средний продукт АРL растет и достигает своего максимума APmax), предельный продукта труда MPL также увеличивается и достигает своего максимального значения MPmax. Затем предельный продукт перестает расти, и, достигая точки своего максимума (иногда ее называют точкой убывания предельного продукта), начинает убывать. При этом средний продукт APL продолжает расти до своего максимального значения (в нашем примере АРL = max при L3).

На втором этапе (от L3 до L4) наблюдается уменьшение отдачи переменного ресурса (т. е. средний продукт АРL убывает), предельный продукт MPL также продолжает сокращаться и достигает нуля (МР = 0 при L4). При этом объем совокупного продукта TP становится максимально (TPmax) возможным и его дальнейшее увеличение за счет прироста только переменных ресурсов уже неосуществимо.

На третьем этапе (начиная с L4 и далее) предельный продукт приобретает отрицательное значение (МР < 0), а совокупный продукт ТР начинает сокращаться.

Для достижения наиболее эффективных результатов и минимизации издержек фирме следует использовать переменный ресурс в объеме, соответствующем II этапу. На I этапе дополнительное использование переменного ресурса ведет к снижению средних издержек. На III этапе сокращаются совокупный объем выпуска и средние издержки (т. е. прибыльность падает).

Причина подобного поведения производственной функции кроется в принципе (законе) убывания предельной отдачи:

начиная с некоторого момента времени, дополнительное использование переменного ресурса при неизменном количестве постоянного ресурса ведет к сокращению предельной отдачи, или предельного продукта.

Данный закон носит универсальный характер и характерен практически для всех экономических процессов. (Русская пословица «У семи нянь дитя без глазу» прекрасно иллюстрирует данный принцип).

d(APL)/dL =   = 0.

Изокванта и карта изоквант. Свойства изоквант

В зависимости от состояния рыночного спроса фирма может выбрать один из нескольких вариантов производства. Для точного определения оптимального объема выпуска используем графический метод анализа производственной функции через изокванты и изокосты.

Построение изокванты

Для простоты анализа, как и прежде, будем полагать, что:

·  исследуемая функция производства зависит от двух факторов: труда и капитала,

·  является частным случаем функции Кобба-Дугласа и имеет вид: Q = KL;

·  факторы производства в определенных пределах будут взаимозаменяемыми;

·  технология производства в течение всего рассматриваемого периода не меняется.

Представим в виде таблицы данную функцию для значений K и L от 1 до 4.

Таблица 6.1 – Производственная функция

L K	1	2	3	4
1	1	2	3	4
2	2	4	6	8
3	3	6	9	12
4	4	8	12	16

Как видно из табл. 6.1, существует несколько комбинаций труда и капитала, обеспечивающих в определенных пределах заданный объем выпуска. Например, Q = 4 можно получить, используя следующие комбинации труда и капитала: (1,4), (4,1) и (2,2). Аналогичным образом Q = 6 можно получить, используя комбинации (2,3) и (3,2), и т. д.

Если отложить по горизонтальной оси количество единиц труда, по вертикальной - количество единиц капитала, затем обозначить точки, в которых фирма выпускает один и тот же объем, то получится кривая, представленная на рис. 6.1 и называемая изоквантой (IQ).

Каждая точка изокванты соответствует комбинации ресурсов, при которой фирма выпускает заданный объем продукции.

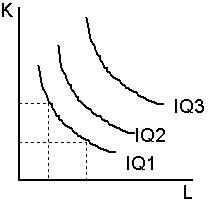
Рисунок 6.1 – Карта изоквант

Набор изоквант, характеризующий данную производственную функцию, называется картой изоквант.

Свойства изоквант

Свойства стандартных изоквант аналогичны характеристикам кривых безразличия.

1) Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек.

2) Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства.

3) Изокванты, описывающие данную производственную функцию, никогда не пересекаются.

Пересечение изоквант противоречило бы условию эффективности производства. Для доказательства этого предположим, что две изокванты для разных объемов имеют одну общую точку А. Отметим на графике еще две произвольные точки В и С, как это изображено на рис. 6.2.

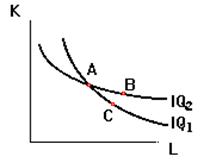
Рисунок 6.2 – Изокванты не пересекаются

Комбинация ресурсов В является более предпочтительной для фирмы, чем комбинация С, поскольку содержит большее количество обоих ресурсов, и следовательно, в соответствии с данной производственной функцией, обеспечивает больший объем выпуска. Вместе с тем комбинации А и В принадлежат одной изокванте, и значит обеспечивают одинаковый объем производства. Комбинации А и С также принадлежат одной изокванте и также обеспечивают одинаковый объем. В соответствии с принципом транзитивности, если А = В и А = С, то и В = С, а это противоречит исходному положению.

4) Изокванты не имеют участков возрастания.

Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого (К), так и второго (L) ресурса, т. е. возрастал бы объем максимального выпуска, а он (объем) должен быть постоянным на всем протяжении изокванты.

Убывающий характер изокванты отражает возможность замещения в определенных пределах используемых ресурсов, так что совокупный объем выпуска остается неизменным.

Предельная норма технологического замещения

Предельная норма технологического замещения (Marginal Rate of Technical Substitution, или MRТS) одного ресурса на другой (например, труда на капитал) показывает степень замещения труда капиталом, при котором объем выпуска остается неизменным.

Алгебраическое выражение, показывающее степень, в которой производитель готов сократить количество капитала в обмен на увеличение труда, достаточную для сохранения прежнего объема выпуска, имеет вид

В силу отрицательного наклона кривой безразличия данное отношение всегда будет величиной отрицательной. Иногда для удобства вводят минус перед правой частью, но в большинстве случаев имеет значение абсолютная величина коэффициента.

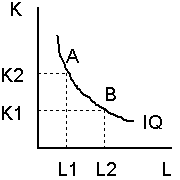
Рисунок 6.3 – Предельная норма технологического замещения

Как видно на рис. 6.3, при переходе из точки А в точку В объем производства остается неизменным. Это означает, что сокращение выпуска в результате уменьшения затрат капитала ( К = К2 – К1) компенсируется увеличением выпуска за счет использования дополнительного количества труда ( L = L2 – L1).

Сокращение выпуска в результате уменьшения затрат капитала равно произведению  К на предельный продукт капитала, или

- К*МРK

Увеличение выпуска за счет использования дополнительного количества труда в свою очередь равно произведению  L на предельный продукт труда, или

L*MPL

Таким образом, можно записать, что

- К*МРK =  L*MPL

Запишем данное выражение по-иному:

- К/ L = MPL/МРK

или

Производственная функция, связывающая между собой количество капитала, труда и объем выпуска, позволяет также рассчитать предельную норму технологического замещения через производную данной функции:

MRТS = dK/dL

Это значит, что графически в любой точке изокванты предельная степень технологического замещения равна тангенсу угла наклона касательной к изокванте в этой точке.

Очевидно, что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты (рис. 6.4). При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, так как все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала.

В дальнейшем MRTS достигает своего предела (MRTS = 0), а изокванта приобретает горизонтальный вид. Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала в точке Е - минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производства данного объема количество труда имеет место в точке А).

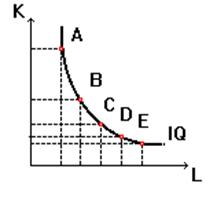
Рисунок 6.4 – Убывание предельной нормы технологического замещения

Убывание MRTS одного ресурса другим характерно для большинства производственных процессов и характерно для всех изоквант стандартного вида.

Особые случаи производственной функции (изокванты нестандартного вида)

Изокванты (как и кривые безразличия) могут иметь различную конфигурацию.

Совершенная взаимозаменяемость ресурсов

Линейная изокванта (рис. 6.5а) предполагает совершенную замещаемостъ производственных ресурсов, так что данный выпуск может быть получен с помощью либо только труда, либо только капитала, либо с использованием различных комбинаций того и другого ресурса при постоянной норме их замещения, т. е. MRTS постоянна во всех точках изокванты.

Примером может служить производство, допускающее как полную автоматизацию, так и ручное изготовление какого-либо продукта.

Фиксированная структура использования ресурсов

Если технологический процесс исключает замещение одного фактора на другой и требует использования обоих ресурсов в строго фиксированных пропорциях, производственная функция (карта изоквант) имеет вид латинской буквы L, как на рис. 6.5б. То есть имеет место жесткая дополняемость ресурсов. Известен лишь один метод производства данного продукта: труд и капитал комбинируются в единственно возможном соотношении, предельная норма замещения равна нулю.

Такую изокванту иногда называют изоквантой леонтьевского типа, по имени американского экономиста русского происхождения В. В. Леонтьева, который положил такой тип изокванты в основу разработанного им метода затраты-выпуск, принесшего ему Нобелевскую премию по экономике.

Примером подобного рода может служить работа землекопа (одна лопата и один человек) или обслуживание башенного крана (один крановщик и один кран). Увеличение количества одного из факторов без соответствующего изменения количества другого фактора невозможно, поэтому технически эффективными (оптимальными) будут лишь угловые комбинации ресурсов.

Наличие нескольких вариантов использования ресурсов

На рис. 6.5в показана ломаная изокванта, предполагающая наличие лишь нескольких методов производства (Р). При этом предельная норма технического замещения при движении вдоль такой изокванты сверху вниз направо убывает.

Изокванта подобной конфигурации используется в линейном программировании – методе экономического анализа, разработанном двумя другими нобелевскими лауреатами – Т. Купмансом (1910-1985) и Л. В.Канторовичем (1912-1986).

Непрерывная, но не совершенная замещаемость ресурсов

Наконец, на рис. 6.5г представлена изокванта, предполагающая возможность непрерывной, но не совершенной замещаемости ресурсов в определенных границах, за пределами которых замещение одного фактора другим технически невозможно (или неэффективно).

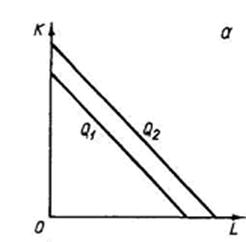
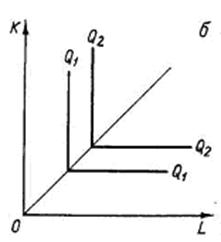
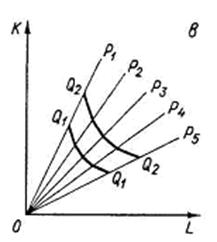
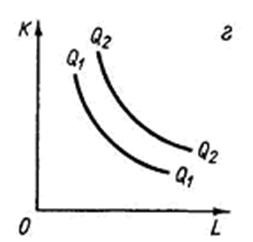
Рисунок 6.5 – Возможные конфигурации изоквант

Многие специалисты, особенно инженеры, предприниматели, вообще те, кого у нас принято называть производственниками, считают ломаную изокванту наиболее реалистично представляющей производственные возможности большинства современных производств. Однако традиционная экономическая теория обычно оперирует гладкими изоквантами, подобными изображенной на рис. 6.5г, поскольку их анализ не требует применения сложных математических методов. Кроме того, изокванты такого вида можно рассматривать как некую приближенную аппроксимацию ломаной изокванты. Увеличивая число методов производства и, следовательно, множество точек излома, мы можем (в пределе) представить ломаную изокванту в виде гладкой кривой.