§8 Туннельный эффект.
Прохождение частицы через потенциальный барьер
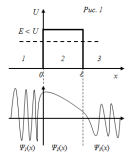
Для классической частицы : при Е > U она пройдет над барьером, при Е < U - отразится от него; для квантовой : при Е > U есть вероятность того, что частица отразится, при Е < U есть вероятность того, что пройдет сквозь барьер.
Потенциальная
энергия: 
Уравнение
Шредингера: для области 1 и 3 : 
для
области 2: 
Решение этих диф. уравнений;
Для
1; 
Для
2; 
Для
3: 
отраженная волна
падающая волна
Временная волновая функция для области 1:
Т.к. в области 3 возможно распределение только прошедшей волны, то, , В3=0.
В области 2 решение зависит от соотношений Е U или Е U. Физический интерес представляет случай Е U.
q = i,
где 
Тогда решение уравнения Шредингера запишутся в виде:
Для 1;
Для
2; 
Для
3: 
Качественный вид функций показан на рис. 2. Из рис. 2 видно, что функция не равна нулю внутри барьера, а в 3 имеет вид волны де Бройля, если барьер не очень широк.
Явление
“проникновения” частицы сквозь
потенциальный барьер, называется туннельным
эффектом. Туннельный
эффект является специфическим квантовым
эффектом. Прохождение частицы можно
объяснить используя соотношения
неопределенностей: неопределенность
импульса р на
отрезке x =
? составляет 
.
Связанная с этим разбросом в значениях
импульса кинетическая энергия 
может
оказаться достаточной для того, чтобы
полная энергия частицы оказалась больше
потенциальной энергии барьера.
§9 Линейный гармонический осциллятор
Линейный гармонический осциллятор - система, совершающая одномерное колебательное движение под действием квазиупругой силы - является моделью для изучения колебательного движения.
В классической физике - это пружинный, физический и математический маятники. В квантовой физике - квантовый осциллятор.
Записав
потенциальную энергию в виде
У
равнение
Шредингера запишется в виде:
Тогда собственные значения энергии:
т.е.
энергия квантового осциллятора принимает
дискретные значения, т.е. квантуется.
Минимальное значение 
-
энергия нулевых колебаний - является
следствием состояния неопределенности
так же, как и в случае частицы в
“потенциальной яме”.
Наличие
нулевых колебаний означает, что частицы
не могут упасть на дно ямы, т.к. в этом
случае был бы точно определен ее
импульс p =
0, p =
0, , x -
не соответствует соотношению
неопределенностей. Наличие энергии
нулевых колебаний противоречит классическим
представлениям, по которым min =
0. 
-
уровни энергии расположенные на равных
расстояниях друг от друга. Из квантового
рассмотрения следует, что частицу можно
обнаружить вне области
.
По классическому рассмотрению только
в пределах –x x x (Рис.2).
Вопрос 50
Энергия кванта |
У всех классических механических волн (в жидкостях, газах и твердых телах) главный параметр, определяющий энергию волны, — это ее амплитуда (точнее, квадрат амплитуды). В случае света амплитуда определяет интенсивность излучения. Однако при изучении явления фотоэффекта — выбивания светом электронов из металла — обнаружилось, что энергия выбитых электронов не связана с интенсивностью (амплитудой) излучения, а зависит только от его частоты. Даже слабый голубой свет выбивает электроны из металла, а самый мощный желтый прожектор не может выбить из того же металла ни одного электрона. Интенсивность определяет, сколько будет выбито электронов, — но только если частота превышает некоторый порог. Оказалось, что энергия в электромагнитной волне раздроблена на порции, получившие название квантов. Энергия кванта электромагнитного излучения фиксирована и равна E = hν, где h = 4·10–15 эВ·с = 6·10–34 Дж·с — постоянная Планка, еще одна фундаментальная физическая величина, определяющая свойства нашего мира. С отдельным электроном при фотоэффекте взаимодействует отдельный квант, и если его энергии недостаточно, он не может выбить электрон из металла. Давний спор о природе света — волны это или поток частиц — разрешился в пользу своеобразного синтеза. Одни явления описываются волновыми уравнениями, а другие — представлениями о фотонах, квантах электромагнитного излучения, которые были введены в оборот двумя немецкими физиками — Максом Планком и Альбертом Эйнштейном. Энергию квантов в физике принято выражать в электрон-вольтах. Это внесистемная единица измерения энергии. Один электрон-вольт (1 эВ) равен энергии, которую приобретает электрон, когда разгоняется электрическим полем напряжением 1 вольт. Это очень небольшая величина, в единицах системы Си 1 эВ = 1,6·10–19 Дж. Но в масштабах атомов и молекул электрон-вольт — вполне солидная величина. От энергии квантов напрямую зависит способность излучения производить определенное воздействие на вещество. Многие процессы в веществе характеризуются пороговой энергией — если отдельные кванты несут меньшую энергию, то, как бы много их ни было, они не смогут спровоцировать надпороговый процесс. Немного забегая вперед, приведем примеры. Энергии СВЧ-квантов хватает для возбуждения вращательных уровней основного электронно-колебательного состояния некоторых молекул, например воды. Энергии в доли электрон-вольта хватает для возбуждения колебательных уровней основного состояния в атомах и молекулах. Этим определяется, например, поглощение инфракрасного излучения в атмосфере. Кванты видимого света имеют энергию 2–3 эВ — этого достаточно для нарушения химических связей и провоцирования некоторых химических реакций, например, тех, что протекают в фотопленке и в сетчатке глаза. Ультрафиолетовые кванты могут разрушать более сильные химические связи, а также ионизировать атомы, отрывая внешние электроны. Это делает ультрафиолет опасным для жизни. Рентгеновское излучение может вырывать из атомов электроны с внутренних оболочек, а также возбуждать колебания внутри атомных ядер. Гамма-излучение способно разрушать атомные ядра, а самые энергичные гамма-кванты даже внедряются в структуру элементарных частиц, таких как протоны и нейтроны. |
VI. Микрочастица в потенциальной яме.
|
Если поместить микрочастицу в бесконечно глубокую потенциальную яму (ограниченная область пространства, в которой потенциальная энергия рассматриваемой частицы меньше, чем вне этого пространства), то волновая функция , описывающая стационарные состояния частицы, будет иметь вид: |
(13)
где ℓ – ширина ямы (ящика);
n – номер энергетического уровня;
x – место положения частицы.
Выражение для собственных значений энергии частицы в глубоком одномерном прямоугольном потенциальном ящике имеет вид:
, (14)
где а = L – ширина ямы,
n = 1, 2, 3…∞ – уровни.
Схема уровней энергии микрочастицы в таком потенциальном ящике и вид функции * показаны на рисунке 3. Минимальное значение энергии микрочастицы в потенциальной яме не равно нулю, то есть она находится в постоянном движении.
Обращает на себя внимание и зависимость плотности вероятности обнаружения микрочастицы на различных расстояниях от стенок ямы от числа n. В дальнейшем n, характеризующее энергетическое (в целом пространственное) положение микрочастицы в потенциальной яме получило название главного квантового числа.
Расстояние между соседними энергетическими уровнями для частиц различной массы m в ящике шириной а составляет:
(15)