§1 Волны де Бройля

В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества - электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

 - волна де Бройля

p =mv- импульс частицы, h - постоянная Планка.

Волны де Бройля, которые иногда называют электронными волнами, не являются электромагнитными.

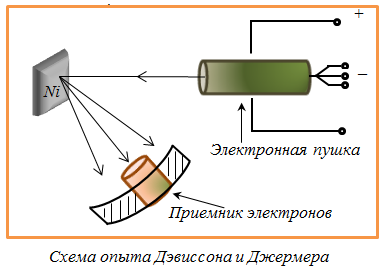
В 1927 году Дэвиссон и Джермер ( амер. физик ) подтвердили гипотезу де Бройля обнаружив дифракцию электронов на кристалле никеля. Дифракционные максимумы соответствовали  формуле Вульфа - Брэггов 2dsin  n, а брэгговская длина волны оказалась в точности равной  .

Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е 50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества - нейтронография и электронография и возникла электронная оптика.

             Макротела также должны обладать всеми свойствами (m = 1кг, следовательно,    ·^ м - невозможно обнаружить современными методами - поэтому макротела рассматриваются только как корпускулы).

 

Свойства волн де Бройля

Пусть частица массы m движется со скоростью v. Тогда фазовая скорость волн де Бройля

.

Т.к. c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме ( v_ф может быть больше и может быть менше с, в отличие от групповой ).

Групповая скорость

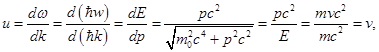
следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

Для фотона

т.е. групповая скорость равная скорости света.

Волны де Бройля испытывают дисперсию. Подставив   в   получим, что v_ф= f(λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10^-26с.

 

§3 Соотношение неопределенностей Гейзенберга

 

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

            Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к.  . Только рассматривая протяженный участок  мы сможем определить импульс частицы. Чем больше , тем точнее р и наоборот, чем меньше , тем больше неопределенность в нахождении р.

            Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

            Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

( иногда записывают       )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

            Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m, тем меньше неопределенности в определении координаты и скорости. При m = 10^-12 кг, ? = 10^-6 и Δx = 1% ?, Δv = 6,62·10^-14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

            Пусть электрон движется в атоме водорода. Допустим Δx ^-10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27·^ м/с. По классической механике при движении по радиусу r  ,·^ м v = 2,3·10^-6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

            Из соотношения   следует, что система имеющая время жизни t, не может быть охарактеризована определенным значением энергии. Разброс энергии   возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность  = h, т.е. спектральные линии будут иметь некоторую ширинуh, будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.