МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Санкт-Петербургский государственный

инженерно-экономический университет»

Кафедра исследования операций в экономике

имени профессора Ю.А. Львова

УТВЕРЖДАЮ

Проректор

по учебно-методической работе

и качеству образования

д.э.н., профессор

_______________ В.И. Малюк

Рег. № Рег. № М-3025

Статистика

Методические указания

к лабораторным работам

для студентов всех формы обучения

Санкт-Петербург

2012

Допущено

редакционно-издательским советом СПбГИЭУ

в качестве методических указаний

Составители

канд. экон. наук В.В.Бродецкая,

канд. экон. наук О.А.Зайцева

асс. О.М.Сувальская

Рецензент

док. экон. наук, проф. В.Н.Соколов

Подготовлено на кафедре

исследования операций в экономике

Имени профессора Юрия Алексеевича Львова

Одобрено

научно-методическим советом СПбГИЭУ

Отпечатано в авторской редакции с оригинал-макета,

представленного составителями

СПбГИЭУ, 2012

Содержание

Общие положения	4
Методические указания к выполнению лабораторной работы №1 «Группировка статистических данных»	5
Методические указания к выполнению лабораторной работы №2 «Обобщающие характеристики совокупности»	12
Методические указания к выполнению лабораторной работы №3 «Статистические методы анализа связи	22
Список литературы	46
Приложение	47

Общие положения

Тематика лабораторных работ охватывает основные темы раздела I «Теория статистики» дисциплины «Статистика». Рабочей программой предусмотрен лабораторный практикум по следующим темам: «Статистическое наблюдение социально-экономических явлений», «Группировка статистических данных», «Статистическое измерение социально-экономических явлений», «Статистические методы анализа взаимосвязей социально-экономических явлений».

Цель методических указаний – научить работать с наиболее доступным и распространенным пакетом обработки статистических данных - ППП MS Excel.

Методические указания к каждой лабораторной работе содержат задание, краткую теоретическую информацию по теме задания и описание процедуры выполнения в ППП MS Excel.

Задания выстроены по мере возрастания сложности, поэтому преподаватель может варьировать степень трудности работы студента с учетом его индивидуальных возможностей.

Самостоятельная работа студента заключается в предварительной подготовке к лабораторной работе: подготовке необходимых статистических данных и изучении соответствующих тем по учебнику или лекционному материалу. Для подготовки к лабораторным работам предлагается использовать учебное пособие «СТАТИСТИКА» коллектива авторов кафедры исследования операций в экономике имени профессора Юрия Алексеевича Львова СПбГИЭУ: Е. А. Андреева, Н.Ю. Вилло, О.А. Зайцева, Г.В. Карпова, Л.И. Курова, М.В. Мироновская, И.Н. Нименья, Н.С. Фещенко

Методические указания дополнены списком рекомендуемой литературы и таблицей статистических данных.

Методические указания к выполнению лабораторной работы №1 Группировка статистических данных

Задание

1. Провести статистическое наблюдение.

2. Построить структурные равноинтервальные группировки для любых трех количественных признаков (в случае необходимости равнонаполненные или произвольные).

3. На основе итоговой группировки построить вариационный и кумулятивный ряды распределения.

4. Представить результаты графически.

5. Охарактеризовать распределение признака и сделать предварительные выводы.

Подготовка к выполнению лабораторной работы

1. По учебнику изучить темы:

• Статистическое наблюдение

• Статистическая сводка

• Группировка

• Ряд распределения

• Статистические графики

2. Уметь группировать статистические данные.

3. Подготовить выборку объемом не менее 40 единиц по 5 количественным признакам, соответствующим целям и задачам исследования.

Каждый из признаков должен существенно варьировать, но база должна оставаться однородной. Для выполнения последующих лабораторных работ требуется выбирать признаки так, чтобы можно было теоретически обосновать три пары взаимозависимых признаков и зависимость одного из признаков от двух или более других. Например, информация о деятельности 40 туристических компаний по 5 показателям: выручка, численность занятых, количество обслуженных клиентов, кредиторская задолженность и балансовая прибыль. Такую информацию можно найти в статистических сборниках, internet, экономической периодике.

Выполнение задания в ППП MS Excel

1. Группировка

Значения каждого из трех признаков должны быть упорядочены, что реализуется с помощью сортировки (отдельно каждого из признаков): выбираем вкладку ДАННЫЕ – СОРТИРОВКА (традиционно по возрастанию).

Для выполнения структурной равноинтервальной группировки сначала определяем величину интервала по формуле:

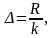
где R – размах вариации, ;

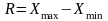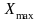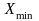- максимальное значение группировочного признака;

- минимальное значение группировочного признака;

k – число групп.

Число групп определяется следующими факторами: задачами исследования, основанием группировки, численностью совокупности, степенью вариации (изменчивости) признака.

Как ориентир для определения количества групп может быть использована формула Стерджесса:

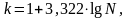
где N – число единиц совокупности.

Если признак варьирует незначительно, может быть взято и меньшее число групп. И наоборот, если вариация велика, для более подробного ее описания лучше выбрать большее число групп.

Далее определяются границы каждого интервала по следующей схеме:

№ интервала	Границы интервала
	нижняя	верхняя
1
2
…
k

Например, пусть статистическая совокупность состоит из 40 туристических компаний, показатели выручки которых варьируют от 50 млн. у.е./год до 650 млн. у.е./год, что является, соответственно, минимальным и максимальным значениями признака. Тогда по формуле Стерджесса получаем: 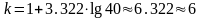. Величина интервала для построения равноинтервальной группировки определяется следующим образом: 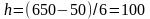(млн.у.е.). Таким образом, совокупность компаний будет разделена по показателю выручки на шесть равных групп: [50-150], [150-250], [250-350], [350-450], [450-550], [550-650] (млн. у.е./год).

После определения границ интервалов рассчитываются частоты, для чего используется функция ЧАСТОТА (вводится как формула массива, т.е. комбинацией клавиш CTRL + SHIFT + ВВОД). Выделяем столбец, в который должны поместиться частоты, соответствующие каждому интервалу. Вызываем функцию (из категории «Статистические») :

= ЧАСТОТА(массив_данных;массив_интервалов)

где массив_данных – это столбец исходных значений признака, для которых вычисляются частоты;

массив_интервалов – это столбец верхних границ интервалов с 1-го по k-1 –й (т.е. без последнего). Функция ЧАСТОТА предполагает формирование верхних границ по принципу «включительно», а нижних – «исключительно».

Сумма частот должна быть равна объему совокупности:

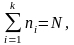
где 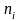- число наблюдений (частота) в i – ой группе.

Далее оценивается относительная структура совокупности через расчет частостей:

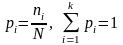
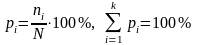
где 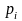- частость в i – ой группе, выраженная в долях единицы или в процентах к итогу.

В результате получаем структурную равноинтервальную группировку.

Группировки с равными интервалами предпочтительнее, но характер изменения большинства социально-экономических явлений не отвечает требованиям, предъявляемым к равноинтервальной группировке.

Если в результате построения равноинтервальной группировки большая часть совокупности попала в один-два смежных интервала, а остальные содержат незначительное число наблюдений, это свидетельствует о том, что исследуемый признак варьирует неравномерно. В данном случае может быть использован «прогрессивный» подход к определению границ интервалов.

В этом случае величина интервалов определяется формулами:

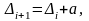
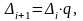
где 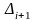- величина i+1 – го интервала;

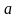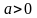– константа арифметической прогрессии, для возрастающих интервалов , для убывающих интервалов ;

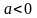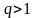q – константа геометрической прогрессии, для возрастающих интервалов , для убывающих интервалов

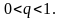
Описанные выше технические способы определения величины интервалов не гарантируют, что не появятся группы малочисленные или вообще «пустые», в которые не попало ни одно наблюдение. Если это произошло, необходимо изменить число групп и/или величины интервалов, так как подобная группировка является некорректной.

Для обеспечения статистической устойчивости показателей, исчисляемых для отдельных групп, может использоваться равнонаполненная группировка, в которой число наблюдений в каждой группе примерно одинаковое и определяется по формуле:

_.

Если полученное n не целое и/или в совокупности есть повторяющиеся значения признака, то число наблюдений в каждой группе может различаться. При этом надо стремиться к тому, чтобы эти различия были незначительны.

Если для реализации задач исследования необходимо устанавливать границы групп там, где количество переходит в новое качество, пользуются специализированными интервалами.

Границы групп могут определяться и произвольно, когда ни один из вышеописанных методов не дал хороших результатов.

2. Ряд распределения

В результате на основе итоговой группировки формируется вариационный ряд распределения (см. табл. 1).

Таблица 1. Ряд распределения выручки туристических компаний, млн. у.е./год

Границы интервала		Частота	Частость	Плотность абсол.	Плотность отснос.
нижняя	верхняя
50	150	12	0,300	0,12	0,00300
150	250	10	0,250	0,10	0,00250
250	350	8	0,200	0,08	0,00200
350	450	5	0,125	0,05	0,00125
450	550	4	0,100	0,04	0,00100
550	650	1	0,025	0,01	0,00025
Итого		40	1	-	-

Для неравноинтервального вариационного ряда распределения сравнение частот по группам неправомерно. В данном случае необходимо избавиться от влияния величины интервала путем перехода от частот/частостей к абсолютной/относительной плотности распределения:

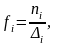
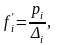
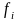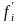где - абсолютная плотность распределения в i – ой группе;

- относительная плотность распределения в i – ой группе;

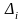- величина i – го интервала.

Далее строится кумулятивный ряд распределения, для чего рассчитываются накопленные частоты/частости к концу каждого интервала:

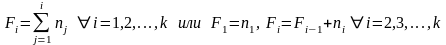
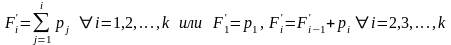
где / 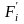- накопленная частота/частость к концу i – ой группы.

3. Графики

Построение гистограммы и кумуляты выполняется с указанием названия графика и каждой оси. Для кумуляты в таблице рассчитываем накопленные частоты/частости (см. табл.2):

где / - накопленная частота/частость к концу i – ой группы.

Таблица 2. Кумулятивный ряд распределения выручки туристических компаний, млн. у.е./год

Границы интервала		Частота		Частость		Накопленная частота		Накопленная частость
нижняя	верхняя
50	150		12		0,30		12		0,300
150	250		10		0,25		22		0,550
250	350		8		0,20		30		0,750
350	450		5		0,13		35		0,875
450	550		4		0,10		39		0,975
550	650		1		0,03		40		1
Итого		40		1		-		-

Гистограмма – графическое изображение интервального вариационного ряда распределения, дающее представление о характере изменения его частот (рис. 1).

Для построения гистограммы выбираем вкладку ВСТАВКА и из разновидностей диаграмм MS Excel - ГИСТОГРАММА. На оси абсцисс откладываются величины интервалов значений признака, на оси ординат – частоты, частости или плотности распределения. Для равноинтервальных рядов могут быть использованы и частоты/частости, и плотности, для неравноинтервальных – только плотности.

Рис. 1. Гистограмма распределения выручки туристических компаний

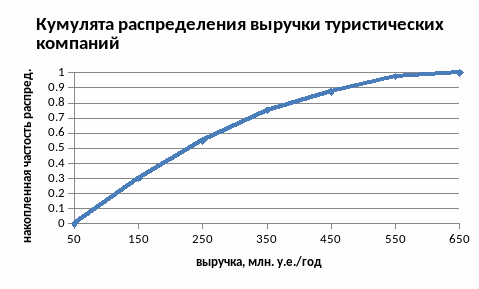
Рис. 2. Кумулята распределения выручки туристических компаний

Кумулята – графическое изображение кумулятивной кривой, дающее представление о характере изменения накопленных частот/частостей (рис. 2).

Для построения кумуляты выбираем ВСТАВКА и из разновидностей диаграмм MS Excel – ТОЧЕЧНАЯ (с прямыми отрезками). На оси абсцисс откладываются величины интервалов значений признака, на оси ординат - накопленные частоты или частости. Равенство или неравенство интервалов для графика кумуляты значения не имеет.

4. Выводы

Выводы должны давать общую картину распределения: однородность совокупности («похожесть» единиц совокупности друг на друга), концентрация значений вокруг средней величины, «типичное» значение, симметричность распределения (преобладание больших или малых значений).