Регрессионный анализ. Множественная линейная регрессия Назначение.

Регрессионная процедура рассчитывает модель зависимости одной переменной-отклика Y от нескольких переменных Xi ,i=1,2....,n.

Y=a 0+a 1*X 1+a 2*X 2+....+a m*X m

по методу наименьших квадратов.

Метод неприменим , если m>30 или n<m+1.

Стандартная выдача результатов регрессионного анализа аналогична рассмотреным в предыдущих примерах.

Многопараметрическая модель не допускает прямого наглядного графического представления, однако для такого представления можно воспользоваться отдельными двумерными сечениями. Для этого необходимо зафиксировать в полученной формуле значения всех независимых переменных, кроме одной. Далее генерируем по этой формуле значение переменной Y, а значение переменной Х генерируем по арифметической прогрессии. Затем по двум полученным в электронной таблице переменным строим функциональный график.

Пример в пакете stadia.

Пример1 : файл MLR содержит 12 значений экспериментальной функции (Y) от двух независимых переменных (X 1, X 2).

X 1 : 0 0 0 0 1 1 1 1 2 2 2 2

X 2 : 0 1 2 3 0 1 2 3 0 1 2 3

Y : 3 4 6 6 4 6 7 8 5 6 7 10

нужно построить линейную модель, предсказать два значения отклика для X 1=1, X 2=2, X 1=2, X 2=4 и выполнить анализ остатков с построением графиков их распределения.

Решение

Множественная линейная регрессия. Файл : mlr.txt

коэффициенты a₀ a₁ a₂

значение 2.88 1.13 1.13

ст. ошибка 0.357 0.211 0.154

значимость 0 0.0007 0

Источник Сум. квадр. Степ. свободы Средн. квадрат.

Регресс. 36.8 2 18.4

Остаточн. 3.21 9 0.356

Вся 40 11

Множеств R R ^2 R^2 прив Ст. ошибка F Значим

959. 0.92 0.90 0.597 51.6 0

Гипотеза 1 : < Регрессионная модель адекватна экспериментальным данным >

Xreg=1, Xreg=2, Y=6.67

Xreg=2, Xreg=4, Y=10.5

Xэксп. Yэксп. Yрегр. остаток Ст.остат. Ст.ошиб. Доверит.инт.

0 3 2.88 0.125 0.231 0.247 0.552

0 4 4.21 -0.208 -0.386 0.247 0.552

0 6 5.54 0.458 0.849 0.247 0.552

0 6 6.88 -0.875 -1.62 0.247 0.552

1 4 4 0 3.37Е-12 0.156 0.349

1 6 5.33 0.667 1.23 0.156 0.349

1 7 6.67 0.333 0.617 0.156 0.349

1 8 8 0 3.37Е-12 0.156 0.349

2 5 5.13 -0.125 -0.231 0.247 0.552

2 6 6.46 -0.458 -0.849 0.247 0.552

2 7 7.79 -0.792 -1.47 0.247 0.552

2 10 9.13 0.875 1.62 0.247 0.552

Г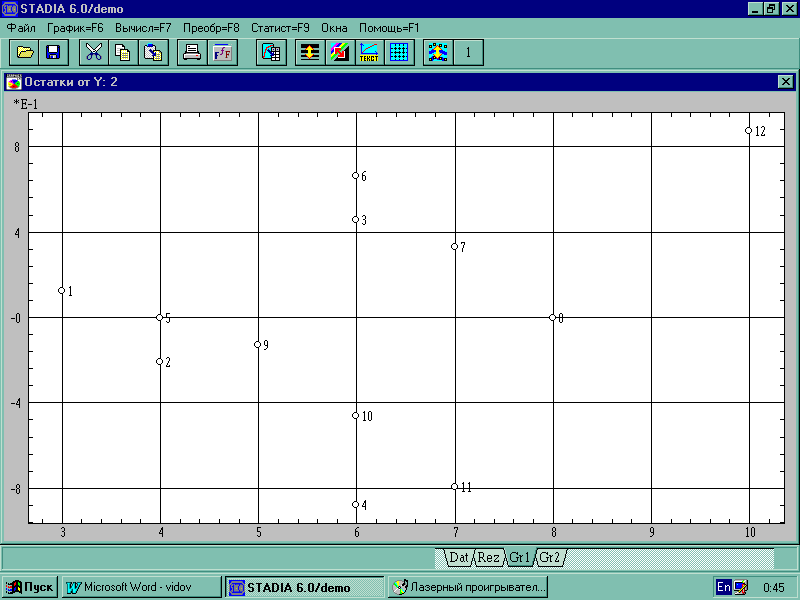 рафик 1 :

Рис.1 Регрессионные остатки ( по оси Y ) относительно регрессионных значений ( по оси X ).

Г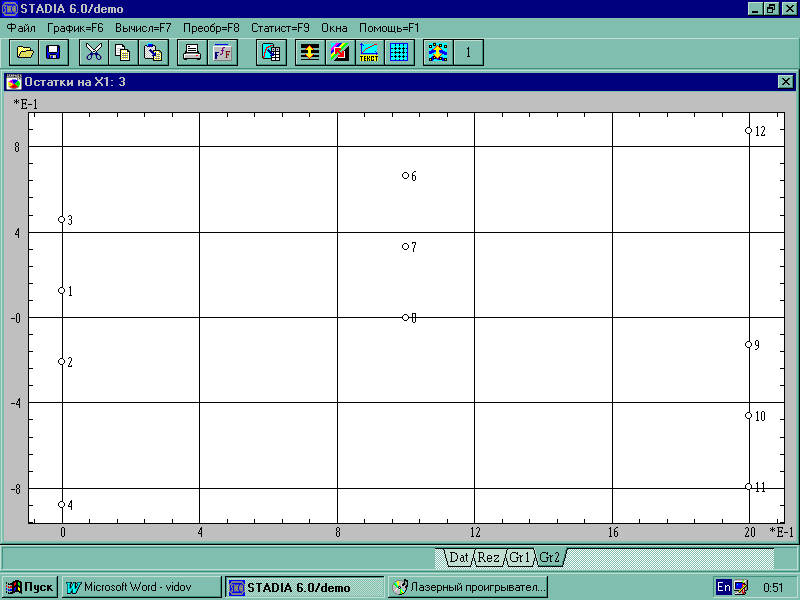 рафик 2.

Рис. 2 Регрессионные остатки ( по оси Y ) относительно значений независимой переменной X₁ ( по оси X ).

Пример 6.2. Руководство авиакомпании по результатам анализа деятельности 15 своих представительств получило следующие данные за март месяц

Y
79,3	2,5	10,0	3,0
200,1	5,5	8,0	6,0
163,2	6,0	12,0	9,0
200,1	7,9	7,0	16,0
146,0	5,2	8,0	15,0
177,7	7,6	12,0	9,0
30,9	2,0	12,0	8,0
291,9	9,0	5,0	10,0
160,0	4,0	8,0	4,0
339,4	9,6	5,0	16,0
159,6	5,5	11,0	7,0
88,3	3,0	12,0	8,0
237,5	6,0	6,0	10,0
107,2	5,0	10,0	4,0
155,0	3,5	10,0	4,0

Где Y (зависимая переменная) – общий доход от проданных билетов, млн. руб.; -средства на развитие компаний в регионе, млн. руб.; - число конкурирующих компаний; - процент пассажиров , летавших бесплатно.

Найти уравнение множественной регрессии. Проверить значимость и адекватность регрессионной модели. Существенно ли влияние на доход число пассажиров, летавших бесплатно? Какой доход ( в среднем) может ожидать компания, вложившая в развитие 2,5 млн. руб., если число конкурирующих компаний в регионе равно десяти, а число пассажиров, летавших бесплатно по разным причинам, составляет 3%. Принять уровень значимости =0,05.