Коэффициенты ранговой корреляции Спирмена и τ Кендалла (Correlations Spearman, Kendall tau).
Задача 1. Спортсмены, ранги которых при построении по росту были 1, 2, ..., 10, заняли на состязаниях следующие места:
6, 5, I, 4, 2, 7, 8, 10, 3, 9.
Как велика ранговая корреляция между ростом и быстротой бега?
НЕПАРАМЕТРИЧЕСКАЯ КОРРЕЛЯЦИЯ.
Переменные: x1, x2
Кендал=0,3333, Z=1,342, Значимость=0,08985, степ.своб = 10
Гипотеза 0: <Нет корреляции между выборками>
Спирмeн=0,4545, Z=1,329, Значимость=0,09191, степ.своб = 10
Гипотеза 0: <Нет корреляции между выборками>
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл: tab.std
Х-лев. Х-станд Частота % Накопл. %
1 -1,486 3 30 3 30
3,25 -0,7432 2 20 5 50
5,5 0 2 20 7 70
7,75 0,7432 3 30 10 100
10 1,486
Колмогоров=0,09552, Значимость=0,1164, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,009866, Значимость=0,1763, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=3,404, Значимость=0,06505, степ.своб = 1
Гипотеза 0: <Распределение не отличается от нормального>
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл: tab.std
Х-лев. Х-станд Частота % Накопл. %
1 -1,486 3 30 3 30
3,25 -0,7432 2 20 5 50
5,5 0 2 20 7 70
7,75 0,7432 3 30 10 100
10 1,486
Колмогоров=0,09552, Значимость=0,1164, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,009866, Значимость=0,1763, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=3,404, Значимость=0,06505, степ.своб = 1
Гипотеза 0: <Распределение не отличается от нормального>
ПАРАМЕТРИЧЕССКАЯ КОРРЕЛЯЦИЯ. Файл:
Переменные: x1, x2
Коэфф.корреляции=0,4545 T:=1,443, Значимость=0,185, степ.своб = 8
Гипотеза 0: <Коэффициент корреляции не отличен от нуля>
Однофакторный дисперсионный анализ.
Задача 1. Проверьте гипотезу о равенстве средних по следующим трем выборкам:
1 |
2 |
3 |
6 5 12 9 10 |
14 11 5 6 — |
12 4 7 — — |
α = 0,05.
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл:
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 3,05 2 1,525 0,1145 0,8925 -0,2497
Остат. 119,9 9 13,32
Общая 122,9 11 11,17
F(фактор1)=0,1145, Значимость=0,8925, степ.своб = 2,9
Гипотеза 0: <Нет влияния фактора на отклик>
Параметры модели:
Среднее = 8,417, доверит.инт.=11,89
Эффект1 = -0,01667, доверит.инт.=20,02
Эффект2 = 0,5833, доверит.инт.=22,38
Эффект3 = -0,75, доверит.инт.=25,84
Задача 2. Проверьте гипотезу о равенстве средних по данным о товарообороте трех магазинов в течение шести месяцев (в млн руб.).
1 |
2 |
3 |
4 2 3 4 5 3 |
6 5 4 7 6 8 |
8 9 10 7 8 6 |
α = 0,10.
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл:
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 61 2 30,5 17,940,0002324 0,1171
Остат. 25,5 15 1,7
Общая 86,5 17 5,088
F(фактор1)=17,94, Значимость=0,0002324, степ.своб = 2,15
Гипотеза 1: <Есть влияние фактора на отклик>
Параметры модели:
Среднее = 5,833, доверит.инт.=5,08
Эффект1 = -2,333, доверит.инт.=8,428
Эффект2 = 0,1667, доверит.инт.=8,428
Эффект3 = 2,167, доверит.инт.=8,428
Парные сравнения Шеффе
Переменные Разность Интервал Значим Гипотеза H1
1-2 2,5 2,035 0,01579 Да
1-3 4,5 2,0350,0002359 Да
2-3 2 2,035 0,05439
x1,x2-x2,x3+: 2,25 1,762 0,007951 Да
x1,x2-x2,x3+: 2,25 1,762 0,007951 Да 2,25 1,762 0,007951 Да
Задача 3. На химическом заводе разработаны два варианта технологического процесса. Чтобы оценить, как изменится дневная производительность при переходе на работу по новым вариантам технологического процесса, завод в течение 10 дней работает по каждому из вариантов.
Дневная производительность завода приводится в таблице:
День работы |
Существующая схема |
Вариант 1 |
Вариант 2 |
1 2 3 4 5 6 7 8 9 10 |
46 48 73 52 72 44 66 46 60 48 |
74 82 64 72 84 68 76 88 70 60 |
52 63 64 48 70 78 68 70 54 75 |
Можно ли считать, что производительность завода изменилась при переходе на новые варианты технологического процесса? Принять α = 0,05.
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
44 -1,019 5 50 5 50
51,25 -0,3766 1 10 6 60
58,5 0,2658 1 10 7 70
65,75 0,9082 3 30 10 100
73 1,551
Колмогоров=0,2468, Значимость=0,1642, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,1051, Значимость=0,08167, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=9,314, Значимость=0,002276, степ.своб = 1
Гипотеза 1: <Распределение отличается от нормального>
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
60 -1,548 2 20 2 20
67 -0,7626 4 40 6 60
74 0,02243 1 10 7 70
81 0,8075 3 30 10 100
88 1,592
Колмогоров=0,1211, Значимость=0,1146, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,0116, Значимость=0,1745, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=3,449, Значимость=0,06331, степ.своб = 1
Гипотеза 0: <Распределение не отличается от нормального>
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
48 -1,615 3 30 3 30
55,5 -0,8673 1 10 4 40
63 -0,1196 4 40 8 80
70,5 0,628 2 20 10 100
78 1,376
Колмогоров=0,1524, Значимость=0,1146, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,03928, Значимость=0,1745, степ.своб = 10
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=3,449, Значимость=0,06331, степ.своб = 1
Гипотеза 0: <Распределение не отличается от нормального>
КРИТЕРИЙ ФИШЕРА И СТЬЮДЕНТА. Файл:
Переменные: сущ, вар1
Статистика Фишера=1,602, Значимость=0,2463, степ.своб = 9,9
Гипотеза 0: <Нет различий между выборочными дисперсиями>
Статистика Стьюдента=4,023, Значимость=0,001073, степ.своб = 18
Гипотеза 1: <Есть различия между выборочными средними>
Стьюдент для парных данных=3,983, Значимость=0,003471, степ.своб = 9
Гипотеза 1: <Есть различия между выборочными средними>
Переменные: сущ, вар2
Статистика Фишера=1,266, Значимость=0,3651, степ.своб = 9,9
Гипотеза 0: <Нет различий между выборочными дисперсиями>
Статистика Стьюдента=1,822, Значимость=0,08199, степ.своб = 18
Гипотеза 0: <Нет различий между выброчными средними>
Стьюдент для парных данных=1,798, Значимость=0,1032, степ.своб = 9
Гипотеза 0: <Нет различий между выброчными средними>
Переменные: вар1, вар2
Статистика Фишера=0,7902, Значимость=0,3653, степ.своб = 9,9
Гипотеза 0: <Нет различий между выборочными дисперсиями>
Статистика Стьюдента=2,262, Значимость=0,03444, степ.своб = 18
Гипотеза 1: <Есть различия между выборочными средними>
Стьюдент для парных данных=2,232, Значимость=0,05061, степ.своб = 9
Гипотеза 0: <Нет различий между выброчными средними>
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл:
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 1676 2 837,9 8,174 0,001998 -0,04635
Остат. 2768 27 102,5
Общая 4444 29 153,2
F(фактор1)=8,174, Значимость=0,001998, степ.своб = 2,27
Гипотеза 1: <Есть влияние фактора на отклик>
Параметры модели:
Среднее = 64,5, доверит.инт.=50,42
Эффект1 = -9, доверит.инт.=68,02
Эффект2 = 9,3, доверит.инт.=68,02
Эффект3 = -0,3, доверит.инт.=68,02
Парные сравнения Шеффе
Переменные Разность Интервал Значим Гипотеза H1
1-2 18,3 11,67 0,002005 Да
1-3 8,7 11,67 0,1757
2-3 9,6 11,67 0,1234
сущ,вар1-вар2: 0,45 12,38 0,9994
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. Файл:
Переменная Размер <---Диапазон---> Среднее---Ошибка Дисперс Ст.откл Сумма
сущ 10 44 73 55,5 3,569 127,4 11,29 555
вар1 10 60 88 73,8 2,82 79,51 8,917 738
вар2 10 48 78 64,2 3,172 100,6 10,03 642
КРИТЕРИИ СДВИГА (ПОЛОЖЕНИЯ). Файл:
Переменные: сущ, вар1
Вилкоксон=67, Критические границы = 83-127, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Ван дер Варден=-5,672, Z=-2,846, Значимость=0,002223, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Для парных данных:
Вилкоксон=1, Критические границы = 11-44, степ.своб = 10
Гипотеза 1: <Есть различия между медианами выборок>
Знаков=1, Z=-2,214, Значимость=0,01344, степ.своб = 2,10
Гипотеза 1: <Есть различия между медианами выборок>
Переменные: сущ, вар2
Вилкоксон=81,5, Критические границы = 83-127, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Ван дер Варден=-3,632, Z=-1,822, Значимость=0,0342, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Для парных данных:
Вилкоксон=15, Критические границы = 11-44, степ.своб = 10
Гипотеза 0: <Нет различий между медианами выборок>
Знаков=4, Z=-0,3162, Значимость=0,3759, степ.своб = 2,10
Гипотеза 0: <Нет различий между медианами выборок>
Переменные: вар1, вар2
Вилкоксон=130, Критические границы = 83-127, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Ван дер Варден=3,937, Z=1,975, Значимость=0,02412, степ.своб = 10,10
Гипотеза 1: <Есть различия между медианами выборок>
Для парных данных:
КРИТЕРИИ МАСШТАБА (РАССЕЯНИЯ). Файл:
Переменные: сущ, вар1
Ансaри-Бредли=52, Z=-0,4553, Значимость=0,3245, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
Клотц=7,735, Z=0,0954, Значимость=0,462, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
Переменные: сущ, вар2
Ансaри-Бредли=48,5, Z=-0,9864, Значимость=0,162, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
Клотц=8,721, Z=0,5991, Значимость=0,2746, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
Переменные: вар1, вар2
Ансaри-Бредли=55, Z=0, Значимость=0,5, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
Клотц=7,501, Z=-0,0242, Значимость=0,4903, степ.своб = 10,10
Гипотеза 0: <Нет различий между выборками в масштабах>
КРИТЕРИЙ КОЛМОГОРОВА-СМИРНОВА. Файл:
Переменные: сущ, вар1
Смирнов=0,7, Значимость=0,01489, степ.своб = 10,10
Гипотеза 1: <Есть интегральные различия между выборками>
Переменные: сущ, вар2
Смирнов=0,5, Значимость=0,1642, степ.своб = 10,10
Гипотеза 0: <Нет интегральных различий между выборками>
Переменные: вар1, вар2
Смирнов=0,4, Значимость=0,4038, степ.своб = 10,10
Гипотеза 0: <Нет интегральных различий между выборками>
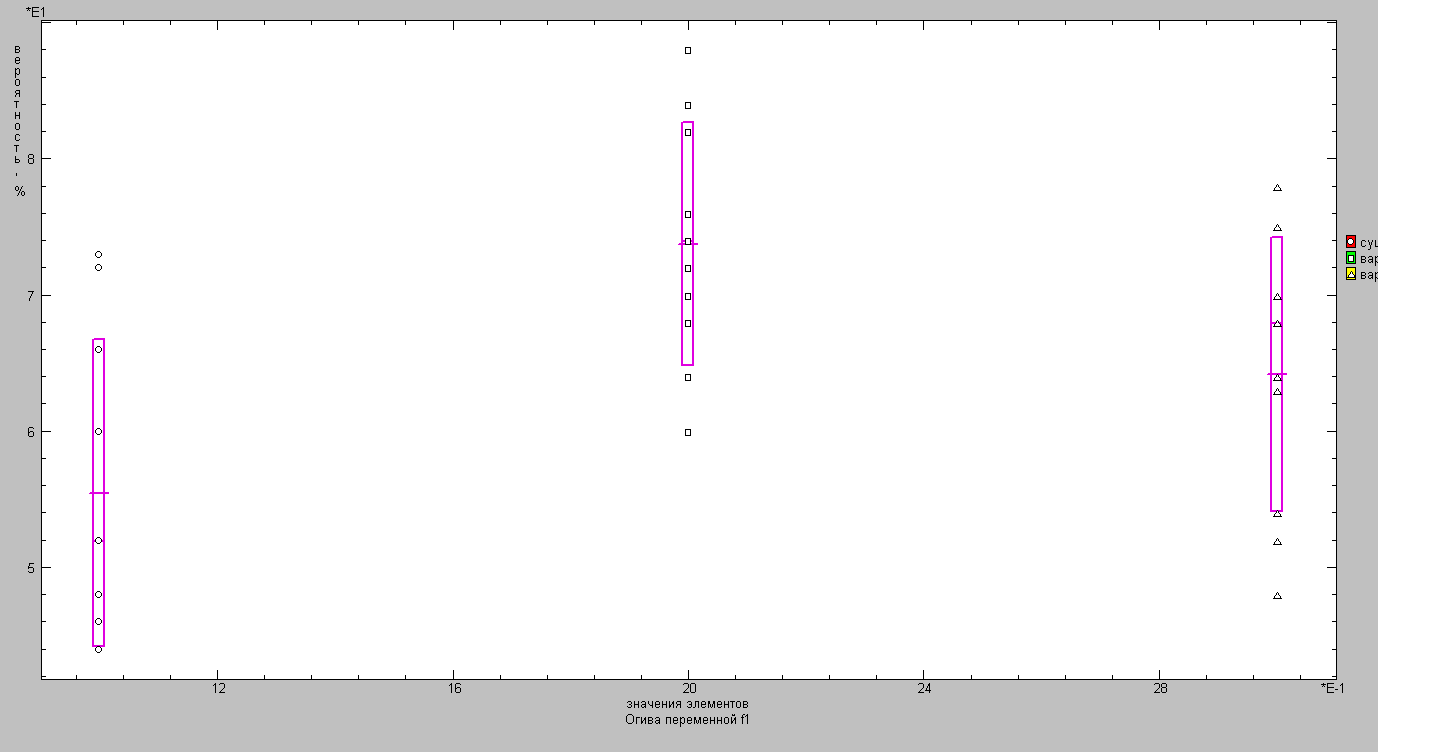
Вывод : лучше воспользоваться вариантом 1
Задача 4. В трех магазинах, продающих товары одного вида, данные
товарооборота за 8 месяцев работы (в тыс. руб.) составили следующую сводку
Магазин |
|
|
|
Месяц |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
19 |
23 |
26 |
18 |
20 |
20 |
18 |
35 |
2 |
20 |
20 |
32 |
27 |
40 |
24 |
22 |
18 |
3 |
16 |
15 |
18 |
26 |
19 |
17 |
19 |
18 |
Требуется проверить гипотезу Н0 о равенстве среднего товарооборота в магазинах. Если гипотеза принимается, то найти несмещенные оценки среднего и дисперсии. Предполагается, что выборки получены из независимых нормально распределенных совокупностей с одной и той же дисперсией. Проверьте, выполняются ли эти предположения.
Принять α= 0,10.
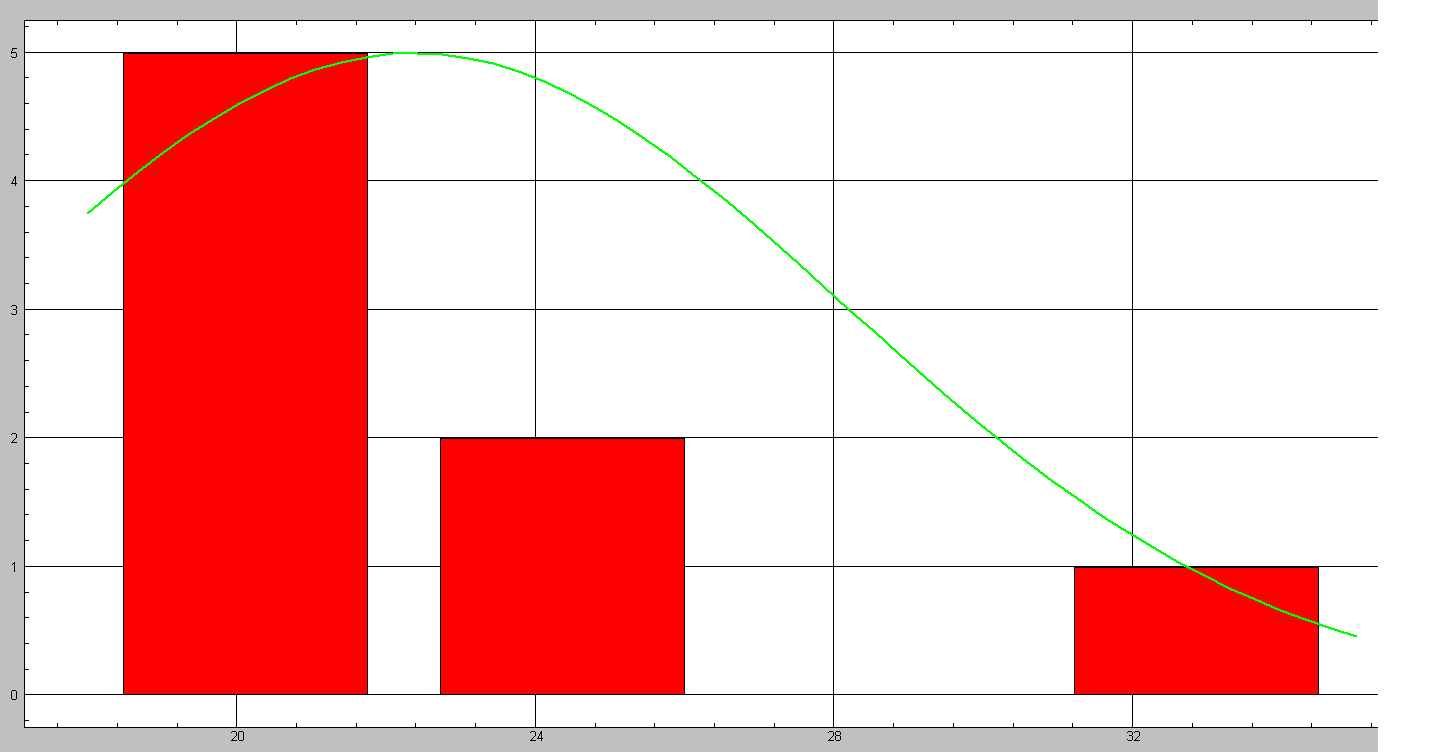
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
18 -0,7569 5 62,5 5 62,5
22,25 -0,02163 2 25 7 87,5
26,5 0,7136 0 0 7 87,5
30,75 1,449 1 12,5 8 100
35 2,184
Колмогоров=0,2844, Значимость=0,1332, степ.своб = 8
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,1166, Значимость=0,05368, степ.своб = 8
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=6,756, Значимость=0,009347, степ.своб = 1
Гипотеза 1: <Распределение отличается от нормального>
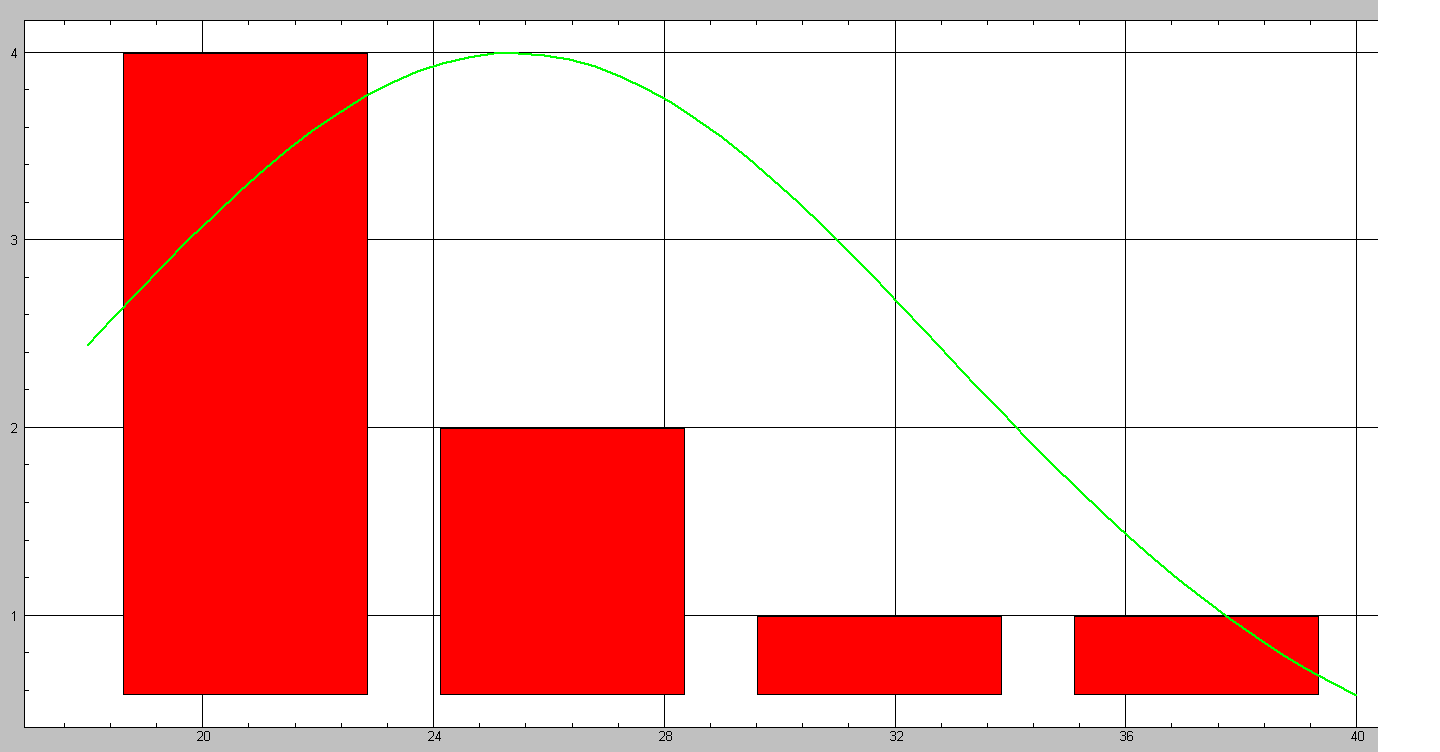
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
18 -0,9933 4 50 4 50
23,5 -0,2525 2 25 6 75
29 0,4882 1 12,5 7 87,5
34,5 1,229 1 12,5 8 100
40 1,97
Колмогоров=0,1985, Значимость=0,1346, степ.своб = 8
Гипотеза 0: <Распределение не отличается от нормального>
Омега-квадрат=0,06068, Значимость=0,3419, степ.своб = 8
Гипотеза 0: <Распределение не отличается от нормального>
Хи-квадрат=3, Значимость=0,08328, степ.своб = 1
Гипотеза 0: <Распределение не отличается от нормального>
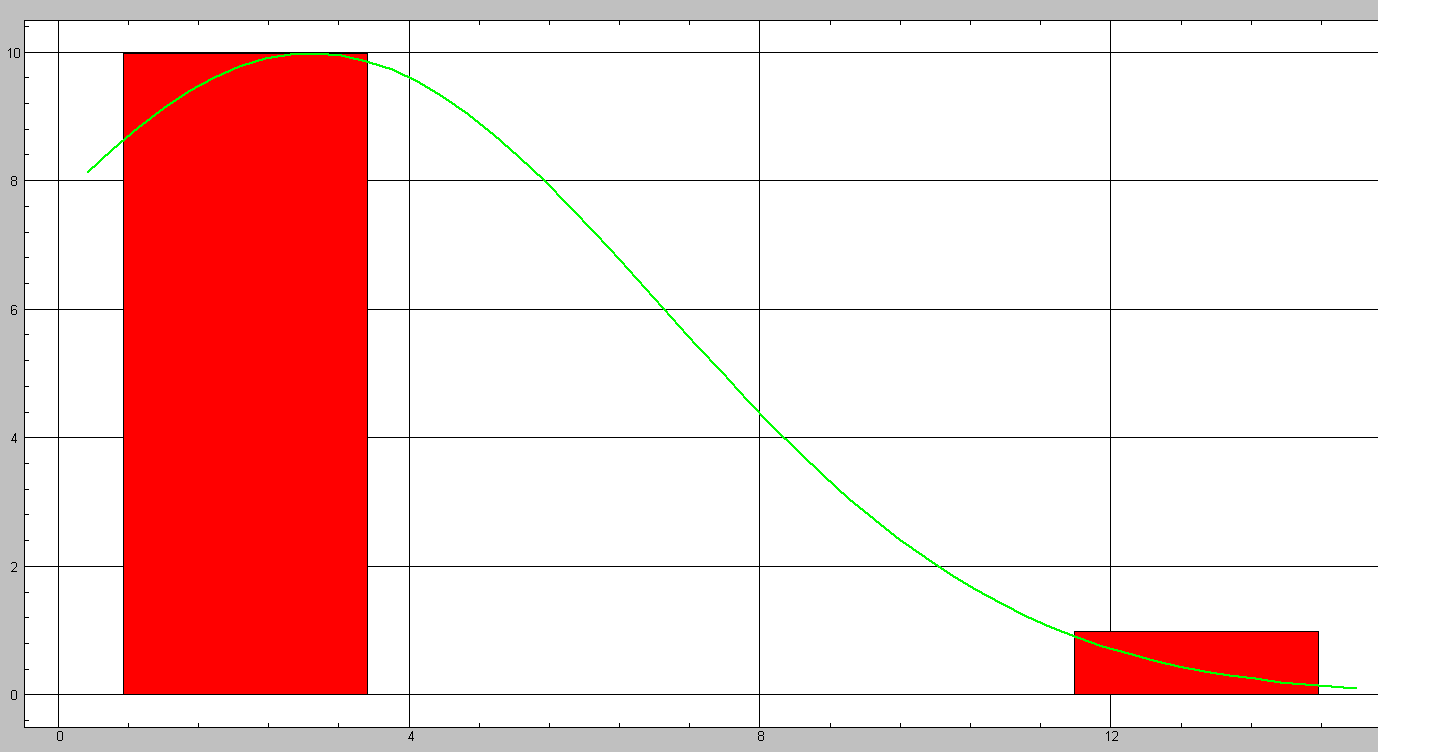
ГИСТОГРАММА И ТЕСТ НОРМАЛЬНОСТИ. Файл:
Х-лев. Х-станд Частота % Накопл. %
3,338 -0,6411 10 90,91 10 90,91
39,5 0,2661 0 0 10 90,91
75,67 1,173 0 0 10 90,91
111,8 2,081 1 9,091 11 100
148 2,988
Колмогоров=0,438, Значимость=4,228E-5, степ.своб = 11
Гипотеза 1: <Распределение отличается от нормального>
Омега-квадрат=0,5447, Значимость=4,958E-8, степ.своб = 11
Гипотеза 1: <Распределение отличается от нормального>
Хи-квадрат=29,42, Значимость=3,138E-6, степ.своб = 1
Гипотеза 1: <Распределение отличается от нормального>
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл:
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 190,1 2 95,04 2,86 0,07826 -0,1077
Остат. 697,8 21 33,23
Общая 887,8 23 38,6
F(фактор1)=2,86, Значимость=0,07826, степ.своб = 2,21
Гипотеза 0: <Нет влияния фактора на отклик>
Параметры модели:
Среднее = 22,08, доверит.инт.=25,75
Эффект1 = 0,2917, доверит.инт.=38,18
Эффект2 = 3,292, доверит.инт.=38,18
Эффект3 = -3,583, доверит.инт.=38,18
Задача 6. Файл А1 в каталоге DAT содержит данные об урожайности четырёх сортов пшеницы на участках одинакового типа почвы. Отличаются ли эти сорта по урожайности.
17 15.8 17.4 15.7
17.2 17 16.6 16.8
16.1 16.4 16.2 15.1
17 ? 15.6 15.2
16.8 ? 15.5 ?
? ? 17.2 ?
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл: a1.std
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 2,824 3 0,9412 2,047 0,1528 -0,1505
Остат. 6,436 14 0,4597
Общая 9,26 17 0,5447
F(фактор1)=2,047, Значимость=0,1528, степ.своб = 3,14
Гипотеза 0: <Нет влияния фактора на отклик>
Параметры модели:
Среднее = 16,37, доверит.инт.=1,819
Эффект1 = 0,4533, доверит.инт.=2,664
Эффект2 = 0,03333, доверит.инт.=3,439
Эффект3 = 0,05, доверит.инт.=2,432
Эффект4 = -0,6667, доверит.инт.=2,978
Задача 7. Файл SHEFFE содержит данные прочности шести сплавов в нескольких испытаниях. Четвёртый сплав является стандартным. Есть ли различия в прочности сплавов.
15.1 15.3 15.1 15.3 15.2 15.2
15 15.5 15.6 14.9 14.8 15.1
15.4 15.7 15.4 15 15.4 15.3
15 15.8 15.7 14.9 15 15.1
? 15.3 ? 15.2 15 ?
? ? ? 14.9 ? ?
Дополнительно сравните группу X2,X3 и группуX1,X5,X6
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл: sheffe.std
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 1,013 5 0,2026 4,874 0,00403 0,02184
Остат. 0,9143 22 0,04156
Общая 1,927 27 0,07138
F(фактор1)=4,874, Значимость=0,00403, степ.своб = 5,22
Гипотеза 1: <Есть влияние фактора на отклик>
Параметры модели:
Среднее = 15,22, доверит.инт.=0,4154
Эффект1 = -0,09643, доверит.инт.=0,676
Эффект2 = 0,2986, доверит.инт.=0,6046
Эффект3 = 0,2286, доверит.инт.=0,676
Эффект4 = -0,1881, доверит.инт.=0,552
Эффект5 = -0,1414, доверит.инт.=0,6046
Эффект6 = -0,04643, доверит.инт.=0,676
Парные сравнения Шеффе
Переменные Разность Интервал Значим Гипотеза H1
1-2 0,395 0,4982 0,1836
1-3 0,325 0,5252 0,4326
1-4 0,09167 0,4794 0,9898
1-5 0,045 0,4982 0,9991
1-6 0,05 0,5252 0,999
2-3 0,07 0,4982 0,9966
2-4 0,4867 0,4497 0,0282 Да
2-5 0,44 0,4697 0,07635
2-6 0,345 0,4982 0,3104
3-4 0,4167 0,4794 0,1172
3-5 0,37 0,4982 0,2411
3-6 0,275 0,5252 0,6118
4-5 0,04667 0,4497 0,9987
4-6 0,1417 0,4794 0,9433
5-6 0,095 0,4982 0,9899
x1,x2,x3-x4,x5,x6: 0,2689 0,3112 0,1138
Дополнительное сравнение групп:
x2,x3-x1,x5,x6: 0,3583 0,3549 0,04134 Да
Дополнительная задача.1.
17 15.8 17.4 15.7
17.2 17 16.6 16.8
16.1 16.4 16.2 15.1
17 ? 15.6 15.2
16.8 ? 15.5 ?
? ? 17.2 ?
Решение:
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл: a1.std
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 2,824 3 0,9412 2,047 0,1528 -0,1505
Остат. 6,436 14 0,4597
Общая 9,26 17 0,5447
F(фактор1)=2,047, Значимость=0,1528, степ.своб = 3,14
Гипотеза 0: <Нет влияния фактора на отклик>
Параметры модели:
Среднее = 16,37, доверит.инт.=1,819
Эффект1 = 0,4533, доверит.инт.=2,664
Эффект2 = 0,03333, доверит.инт.=3,439
Эффект3 = 0,05, доверит.инт.=2,432
Эффект4 = -0,6667, доверит.инт.=2,978
Дополнительная задача 2 .
15.1 15.3 15.1 15.3 15.2 15.2
15 15.5 15.6 14.9 14.8 15.1
15.4 15.7 15.4 15 15.4 15.3
15 15.8 15.7 14.9 15 15.1
? 15.3 ? 15.2 15 ?
? ? ? 14.9 ? ?
Решение:
(Однофакторный дисперсионный анализ Шеффе6454654x1x2x3x4x5x615.11515.41515.315.515.715.815.315.115.615.415.715.314.91514.915.214.915.214.815.4151515.215.115.315.1
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл: sheffe.std
параметрический
Источник Сум.квадр Ст.своб Ср.квадр F Значимость Сила влияния
Факт.1 1,013 5 0,2026 4,874 0,00403 0,02184
Остат. 0,9143 22 0,04156
Общая 1,927 27 0,07138
F(фактор1)=4,874, Значимость=0,00403, степ.своб = 5,22
Гипотеза 1: <Есть влияние фактора на отклик>
Параметры модели:
Среднее = 15,22, доверит.инт.=0,4154
Эффект1 = -0,09643, доверит.инт.=0,676
Эффект2 = 0,2986, доверит.инт.=0,6046
Эффект3 = 0,2286, доверит.инт.=0,676
Эффект4 = -0,1881, доверит.инт.=0,552
Эффект5 = -0,1414, доверит.инт.=0,6046
Эффект6 = -0,04643, доверит.инт.=0,676
Парные сравнения Шеффе
Переменные Разность Интервал Значим Гипотеза H1
1-2 0,395 0,4982 0,1836
1-3 0,325 0,5252 0,4326
1-4 0,09167 0,4794 0,9898
1-5 0,045 0,4982 0,9991
1-6 0,05 0,5252 0,999
2-3 0,07 0,4982 0,9966
2-4 0,4867 0,4497 0,0282 Да
2-5 0,44 0,4697 0,07635
2-6 0,345 0,4982 0,3104
3-4 0,4167 0,4794 0,1172
3-5 0,37 0,4982 0,2411
3-6 0,275 0,5252 0,6118
4-5 0,04667 0,4497 0,9987
4-6 0,1417 0,4794 0,9433
5-6 0,095 0,4982 0,9899
x1,x2,x5-x3,x4,x6: 0,02222 0,3112 0,9998
Дополнительная задача 3.
40 38 48
35 40 40
38 47 45
43 44 43
44 40 46
41 42 44
? ? ?
%Однофакт.дисперс. непараметрич.анализ3666x1x2x3403538434441384047444042484045434644
1-ФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. Файл: jon.std
Краскал-Уоллис=4,361, Значимость=0,113, степ.своб = 2
Гипотеза 0: <Нет влияния фактора на отклик>
Джонкхиер=79, Значимость=0,02164, степ.своб = 3,18
Гипотеза 1: <Есть влияние фактора на отклик>
Ответ: нет, не влияла.