
- •Нелинейные методы и модели в экономике.
- •Глава 6. Постановки знп и основные определения…………………………..3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •Глава 9. Выпуклый анализ
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2.Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то полагаем и идем на выход. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •2.1. Постановки злп
- •3.1. Определение двойственной задачи
- •3.5. Анализ решения из и дз на основе отчетов ms Excel
- •4.1. Постановки транспортной задачи
- •4.4 Опорный план тз. Алгоритм нахождения исходного плана
- •4.5. Метод потенциалов решения транспортной задачи
- •4.6. Задача о назначениях
- •5.2. Метод ветвей и границ решения задач целочисленного программирования
- •5.3. Задача коммивояжера
Метод хорд (секущих)
При реализации этого метода учитывается не только знак производной, но и ее значение. Метод заключается в решении уравнения методом хорд и носит потому то же название.
Предполагаем, как и в предыдущем разделе, что знаки производной унимодальной функции на концах отрезка различны: ; .
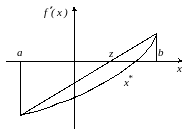
Тогда приближение к стационарной точке определится по формуле
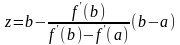 (7.4)
(7.4)
Алгоритм метода хорд тот же, что и алгоритм метода средней точки за исключением того, что координата точки вычисляется по формуле (7.4).
В качестве примера рассмотрим две итерации вычисления координаты точки максимума функции на отрезке .
.
Итерация 1
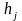 ;
;
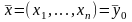 ;
;
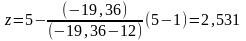 ;
;
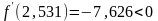 ;
;
 .
.
Итерация 2
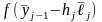 ;
;
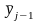 ;
;
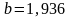 .
.
Метод кубической аппроксимации
В
соответствии с этим методом предполагается,
что функция
,
которая подлежит максимизации, хорошо
аппроксимируется на отрезке
 полиномом третьей степени. Построим
этот полином по заданным значениям
функции
полиномом третьей степени. Построим
этот полином по заданным значениям
функции
 и
и
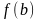 и ее производной
и ее производной
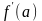 и
и
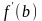 (полином Эрмита) в виде
(полином Эрмита) в виде
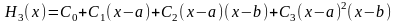 .
.
Коэффициенты
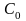 ,
,
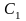 ,
,
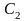 ,
,
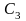 ,
определяемые из условий
,
определяемые из условий
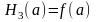 ;
;
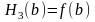 ;
;
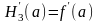 ;
;
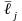 ,
равны:
,
равны:
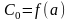 ;
; 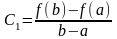 ;
;
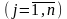 ;
; 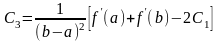 .
.
Точку максимума оценим точкой интерполяционного полинома, для чего приравняем производную полинома нулю:
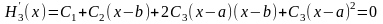 .
.
Решая это квадратное уравнение, получим
 , (7.5)
, (7.5)
где
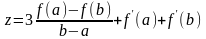 ; (7.6)
; (7.6)
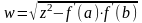 . (7.7)
. (7.7)
Алгоритм метода кубической аппроксимации
Исходные
данные.
 – отрезок, содержащий точку максимума
,
,
,
– отрезок, содержащий точку максимума
,
,
,
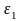 ,
, – параметры окончания счета.
– параметры окончания счета.
Если
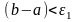 ,
то
,
то
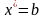 ,
конец.
,
конец.Вычислить
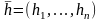 по формулам (7.4)-(7.7).
по формулам (7.4)-(7.7).Вычислить ;
 .
.Если
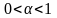 ,
то
,
то
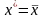 ,
конец.
,
конец.Если
 ,
то
,
,
то
,
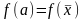 ,
,
 ;
перейти к шагу 1.
;
перейти к шагу 1.;
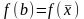 ;
;
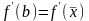 ;
перейти к шагу 1.
;
перейти к шагу 1.
Пример
7.6.
Найти точку максимума функции
на отрезке
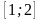 ;
;
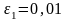 ;
;
 .
.
.
Итерация 1
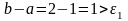 ;
;
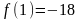 ;
;
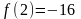 ;
;
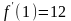 ;
;
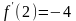 ;
;
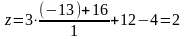 ;
;
;
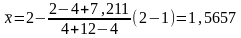 ;
;
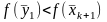 ;
;
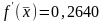 .
.
Так
как
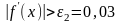 ,
продолжаем расчет.
,
продолжаем расчет.
,
следовательно,
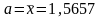 .
.
Итерация 2
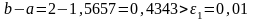 ;
;
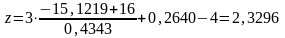 ;
;
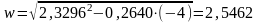 ;
;
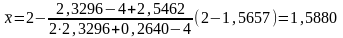 ;
;
 ;
;
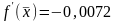 .
.
Так
как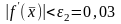 ,
следовательно,
,
следовательно,
 .
.
7.5. Методы второго порядка. Метод Ньютона-Рафсона
Предполагаем,
что унимодальная функция
дважды непрерывно дифференцируема.
Тогда для решения уравнения
можно применить метод касательных
(Ньютона)
 ,
,
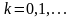 (7.8)
(7.8)
Алгоритм метода Ньютона-Рафсона
Исходные
данные.
-начальная
оценка координаты стационарной точки,
,
– параметр окончания счета,
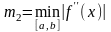
.
.
Если
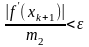 ,
то
,
то
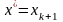 ,
конец.
,
конец., перейти к шагу 2.
Пример
7.7. Найти точку максимума функции
на отрезке
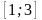 ,
,
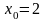 ,
,
 .
.
Итерация 1
 ;
;
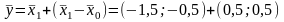 ;
;
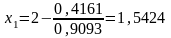 ;
;
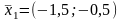 .
.
Итерация 2
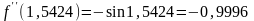 ;
;
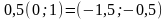 ;
;
 ,
,
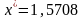 .
.
Последовательность (7.8) сходится к стационарной точке лишь при выполнении определенных условий, накладываемых на вид функции и выбор начальной точки (теорема о сходимости метода касательных).
Глава 8. Графический метод решения знп.
8.1. Алгоритм графического метода решения знп
Рассмотрим задачу НП
(8.1)
(8.2)
(8.3)
(8.4)
где - определенные на функции, из которых хотя бы одна является нелинейной, .
Рассмотрим примеры решения ЗНП с двумя переменными. Так же как и в случае задачи линейного программирования, они могут быть решены графически.
Алгоритм графического метода решения ЗНП.
Шаг 1. Строим область допустимых решений – область Р, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗНП (8.2-8.4)( если она пуста, то ЗНП не имеет решения).
Шаг
2.
Строим линию уровня (гиперповерхность)
функции 8.1:
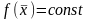 .
.
Шаг 3. Определяем гиперповерхность наивысшего (наинизшего) уровня или устанавливаем неразрешимость ЗНП из-за неограниченности функции 8.1 сверху (снизу) на множестве Р.
Шаг 4. Находим точку области Р, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяем в ней значение функции 8.1.
В отличие от ЗЛП решение ЗНП может достигаться как внутри области Р (пример 8.3), так и на границе: в угловой точке (пример 8.2, 8.3, 8.5) или в неугловой точке (пример 8.1, 8.2, 8,4).
