12.4.4. Метод Дэвидона-Флетчера-Пауэлла Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде

,

где - положительно определённая симметрическая матрица. Метод ДФП основан на использовании идей метода Ньютона и методов, использующих сопряжённые направления. В методе ДФП матрицы рекуррентно определяются так, чтобы последовательные приближения

минимизировали квадратичную функцию за конечное число шагов.

В отличие от метода Ньютона в методе ДФП используется только первые производные и не требуется на каждом шаге обращать матрицу . Кроме того, рекуррентные соотношения для матрицы строятся таким образом, чтобы последовательность матриц сходилась к .

Алгоритм метода дфп

Начальный этап. Задать начальную точку и симметрическую положительно определённую матрицу . Положить , . Задать - параметр окончания счёта.

Основной этап.

Шаг 1. Вычислить .

Шаг 2. Вычислить , положить .

Шаг 3. Если , то перейти к шагу 5.

Шаг 4. Вычислить , , ; , положить и перейти к шагу 1.

Шаг 5. Положить . Если , то положить и остановиться, иначе положить , , и перейти к шагу 1.

В условиях алгоритма ДФП справедлива теорема.

Теорема 12.4. Направления ( ), генерируемые алгоритмом ДФП, являются направлениями спуска, а матрицы ( )- симметрическими и положительно определёнными.

Теперь рассмотрим задачу безусловной оптимизации квадратичной функции:

, , (12.18)

где - симметрическая положительно определённая матрица.

Теорема 12.5. Пусть задача (12.18) решается методом ДФП. Тогда, если для всех , то

1. направления являются - сопряжёнными;

2. -является решением задачи (2.18);

3. .

Из теоремы 12.5. следует, что задача (12.18) с помощью алгоритма ДФП решается за одну итерацию .

Пример 12.11. Найти минимум функции

.

Начальный этап. Пусть , , положим , , вычислим .

Основной этап.

Итерация 1

.

Шаг 1. Вычислим .

Шаг 2. Вычислим , тогда .

Шаг 3. Так как , то переходим к шагу 4.

Шаг 4. Вычислим , , .

.

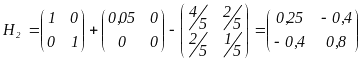Положим и перейдём к шагу 1.

Шаг 1. Вычислим .

Шаг 2.Вычислим , тогда .

Шаг 3. Так как , то переходим к шагу 5.

Шаг 5. Положим . Так как , то - решение задачи.

Покажем, что матрица , которая была бы получена на шаге 4, равна . Действительно, так как , то .

С другой стороны, по формулам шага 4 имеем ; .

,

,

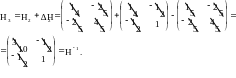
12.4.5. Метод сопряжённых градиентов Флетчера-Ривса

Метод Флетчера-Ривса основан на теореме 12.1, т. е. поиск решения осуществляется вдоль сопряжённых направлений. В отличие от метода ДФП, в котором направление поиска отклоняется от направления наискорейшего спуска в результате умножения на матрицу , в методе Флетчера-Ривса отклонение от направления наискорейшего спуска происходит в результате добавления к нему с некоторым коэффициентом направления, используемого на предыдущем шаге.

Алгоритм метода Флетчера-Ривса

Начальный этап. Задать начальную точку , - параметр окончания счёта, положить , , .

Основной этап.

Шаг 1. Если , то положить и остановиться.

Шаг 2. Вычислить , положить .

Шаг 3. Если , то перейти к шагу 5.

Шаг 4. Вычислить и , положить и перейти к шагу 1.

Шаг 5. Положить , , , и прейти к шагу 1.

Рассмотрим применение метода Флетчера-Ривса к задаче (12.18).

Теорема 12.6. Пусть задача (12.18) решается методом Флетчера-Ривса. Тогда, если для всех , то справедливы следующие утверждения:

1. направления являются - сопряжёнными;

2. направления являются направлениями спуска;

3. - решение задачи (12.18).

Из теоремы 12.6 следует что методом Флетчера-Ривса задача (12.18) решается за одну итерацию , т. е. не более чем за одномерных поисков. При оптимизации неквадратичных функций согласно алгоритму Флетчера-Ривса после реализации каждой - ой итерации ( одномерных поисков) происходит корректировка начального направления, полагается равным , т. е. направлению наискорейшего спуска. Такое периодическое обновление направления поиска, с одной стороны, позволяет уменьшить вероятность построения линейно-зависимых направлений, уменьшает нарастающую погрешность действий, но, с другой стороны, может повлечь за собой замедление сходимости.

Пример 12.12. Найти минимум функции методом Флетчера-Ривса.

.

Начальный этап. Пусть , , ; положим .

Основной этап.

Шаг 1. Вычислим , поэтому переходим к шагу 2.

Шаг 2. Вычислим , положим .

Шаг 3. Так как , то переходим к шагу 4.

Шаг 4. Вычислим , ; , положим и перейдём к шагу 1.

Шаг 1. Так как , то переходим к шагу 2.

Шаг 2. Вычислим , положим .

Шаг 3. Так как , то переходим к шагу 5.

Шаг 5. Положим , , , , и перейдём к шагу 1.

Шаг 1. Так как , то - решение задачи.