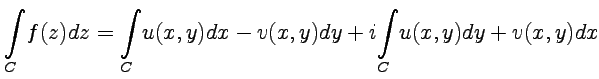- •Определение комплексного числа. Действия с комплексными числами, записанными в алгебраической форме. Умножение и деление комплексных чисел, записанных в алгебраической форме.
- •Определение комплексного числа. Действия с комплексными числами, записанными в тригонометрической форме. Умножение и деление комплексных чисел, записанных в тригонометрической форме.
- •Определение комплексного числа. Действия с комплексными числами, записанными в показательной форме. Умножение и деление комплексных чисел, записанных в показательной форме.
- •Возведение в степень и извлечение корня из комплексного числа.
- •Геометрическая интерпретация комплексных чисел.
- •6. Последовательности комплексных чисел. Основные свойства сходящихся последовательностей комплексных чисел.
- •Последовательности комплексных чисел. Критерий Коши.
- •8. Подпоследовательности последовательности комплексных чисел. Теорема Больцано-Вейерштрасса.
- •Ряды комплексных чисел. Абсолютная и условная сходимость ряда.
- •10. Определение функции комплексного переменного. Вещественная и мнимая части функции комплексного переменного.
- •11. Определение функции комплексного переменного. Предел и непрерывность функции комплексного переменного.
- •12. Непрерывные функции комплексного переменного. Свойства непрерывных функций комплексного переменного.
- •13. Производная и дифференциал. Правила дифференцирования.
- •14. Необходимое и достаточное условие дифференцируемости функции комплексного переменного.
- •15. Линейная функция.
- •16. Функциональные ряды. Признак Вейерштрасса о равномерной сходимости ряда.
- •17. Степенные ряды. Теоремы Абеля о сходимости степенного ряда.
- •18. Определение интеграла от функции комплексного переменного.
14. Необходимое и достаточное условие дифференцируемости функции комплексного переменного.
Для
того чтобы функция ![]() ,
определённая в некоторой области
,
определённая в некоторой области ![]() комплексной
плоскости, была дифференцируема в
точке
комплексной
плоскости, была дифференцируема в
точке ![]() как
функция комплексного переменного
как
функция комплексного переменного ![]() ,
необходимо и достаточно, чтобы её
вещественная и мнимая части
,
необходимо и достаточно, чтобы её
вещественная и мнимая части ![]() и
и ![]() были
дифференцируемы в точке
были
дифференцируемы в точке ![]() как
функции вещественных переменных
и
и
чтобы, кроме того, в этой точке выполнялись
условия Коши — Римана:
как
функции вещественных переменных
и
и
чтобы, кроме того, в этой точке выполнялись
условия Коши — Римана:
![]()
![]()
Компактная запись:
![]()
Если
условия Коши — Римана выполнены, то
производная ![]() представима
в любой из следующих форм:
представима
в любой из следующих форм:
![]()
15. Линейная функция.

16. Функциональные ряды. Признак Вейерштрасса о равномерной сходимости ряда.
Ряд,
членами которого являются функции
комплексного переменного ![]() ,
определенные на некотором
множестве
,
определенные на некотором
множестве ![]() комплексной
плоскости, называется функциональным
рядом в комплексной плоскости и
обозначается
комплексной
плоскости, называется функциональным
рядом в комплексной плоскости и
обозначается
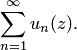
Последовательность ![]() ,
где
,
где 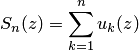 ,
называется последовательностью частичных
сумм ряда (3.1), где
,
называется последовательностью частичных
сумм ряда (3.1), где ![]() —
частичные суммы.
—
частичные суммы.
Ряд
(3.1) называется сходящимся ни множестве ![]() ,
если на множестве
сходится
последовательность его частичных сумм,
т.е. существует предел этой последовательности,
который называется суммой ряда
,
если на множестве
сходится
последовательность его частичных сумм,
т.е. существует предел этой последовательности,
который называется суммой ряда ![]()
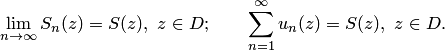
Теорема
Вейерштрасса.
Если для функционального ряда ![]() (1)
можно указать такой сходящийся числовой
ряд
(1)
можно указать такой сходящийся числовой
ряд ![]() ,
что для всех n
,
что для всех n![]() и
для всех
и
для всех ![]() выполняется
условие
выполняется
условие ![]() (2),
то ряд (1) сходится
абсолютно и равномерно на множестве
Е.
(2),
то ряд (1) сходится
абсолютно и равномерно на множестве
Е.
17. Степенные ряды. Теоремы Абеля о сходимости степенного ряда.
Степенным
рядом называется функциональный ряд,
члены которого образованы степенями ![]() или
или ![]() ,
то есть ряд вида
,
то есть ряд вида
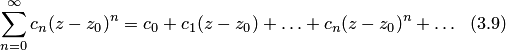
или
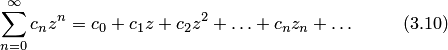
Теорема
Абеля. Если
степенной ряд сходится в точке ![]() ,
то он сходится, и притом абсолютно, для
любого
,
то он сходится, и притом абсолютно, для
любого ![]() ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству ![]() .
.
18. Определение интеграла от функции комплексного переменного.
Пусть на комплексной
плоскости задана кривая |
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
||||
где ![]() .
Учитывая, что
.
Учитывая, что ![]() и,
следовательно,
и,
следовательно, ![]() ,
а также
,
а также ![]() ,
после подстановки интеграл может быть
записан в форме:
,
после подстановки интеграл может быть
записан в форме:
|