Определение комплексного числа. Действия с комплексными числами, записанными в алгебраической форме. Умножение и деление комплексных чисел, записанных в алгебраической форме.
Ко́мпле́ксные чи́сла —
числа вида 
,
где 
и 
—
вещественные числа, 
— мнимая
единица; то есть 
.
Действия над комплексными числами
Сравнение
означает,
что 
и 
(два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение
Вычитание
Умножение
Деление
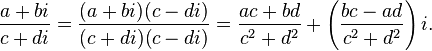
В частности,
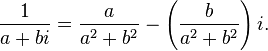
Определение комплексного числа. Действия с комплексными числами, записанными в тригонометрической форме. Умножение и деление комплексных чисел, записанных в тригонометрической форме.
Тригонометрической
формой комплексного числа
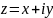является
,
где значение аргумента
,
удовлетворяющее условию
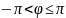
и
,
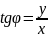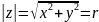– модуль комплексного числа.
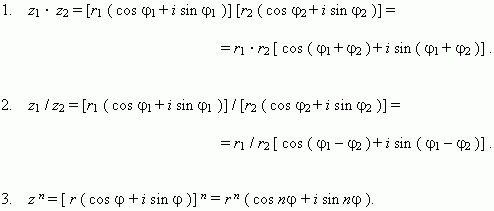
Здесь k - целое. Чтобы получить n различных значений корня n-ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .
Определение комплексного числа. Действия с комплексными числами, записанными в показательной форме. Умножение и деление комплексных чисел, записанных в показательной форме.
Формула
Эйлера (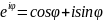
)
позволяет
представить комплексное число 
в
показательной форме:
Такая
форма представления позволяет дать
наглядную интерпретацию операциям
умножения комплексных чисел, их деления
и возведения комплексного числа в
степень. Например, умножение комплексного
числа 
на
комплексное число 
сводится
к повороту вектора, соответствующего
числу 
,
на угол 
и
изменению его длины в 
раз:
Другими словами,
чтобы найти произведение комплексных
чисел, нужно перемножить их модули и
сложить аргументы.
Аналогично
интерпретируется частное от деления
комплексного числа
на
комплексное число
:
где
и
Для
возведения комплексного числа z
в целую степень n нужно
представить это число в показательной
форме, возвести обе части равенства 
в
степень n и
записать результат в тригонометрической
форме:
Если
число 
в
левой части этого равенства представить
в тригонометрической форме и сократить
общий множитель 
,
то получится формула
Муавра:
.
Возведение в степень и извлечение корня из комплексного числа.
Формула Муавра для возведения в целую степень комплексного числа:
Извлечение корня из комплексного числа:
Геометрическая интерпретация комплексных чисел.
Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой.
Расстояние r точки z от нулевой точки, т. е. число
называется модулем комплексного числа z и обозначается символом |z|.
Число
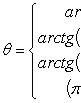
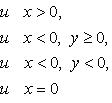
называем аргументом комплексного числа z и обозначаем символом θ = arg z.
6. Последовательности комплексных чисел. Основные свойства сходящихся последовательностей комплексных чисел.
Основные понятия, связанные с последовательностями комплексных чисел, вводятся так же, как в действительной области.
1. Если
каждому натуральному числу 
поставлено
в соответствие комплексное число 
,
то говорят, что задана последовательность
комплексных чисел (последовательность
с комплексными членами): 
.
2. Последовательность 
называется
ограниченной, если существует число 
,
такое, что для любого
выполняется
неравенство 
.
Последовательность, не являющаяся
ограниченной, называется неограниченной:
для 
,
что 
.
3. Последовательность
называется
бесконечно малой, если для любого
числа 
найдется
номер 
,
такой, что для всех 
,
удовлетворяющих условию 
,
выполняется неравенство 
4. Последовательность
называется
бесконечно большой, если для любого
числа 
найдется
номер 
,
такой, что для всех
,
удовлетворяющих условию 
,
выполняется неравенство 
.
5. Число 
называется
пределом последовательности
,
если последовательность 
является
бесконечно малой (обозначается 
):
для
.
6. Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, — расходящейся.
Основные свойства сходящихся последовательностей комплексных чисел:
