Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:

Lрез = 1 / ?2С, Срез = 1 / ?2L

Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур. 

Пример полезного применения резонанса напряжений: входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной. 

Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение_ напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.

2 Условием возникновения резонанса напряжений в последовательном RLC - контуре является равенство реактивных сопротивлений катушки и конденсатора. При   значения противоположных по фазе напряжений на индуктивности и на емкости равны, поэтому резонанс в рассматриваемой цепи называют резонансом напряжений. Полное сопротивление последовательного контура при резонансе минимально и равно активному сопротивлению. Из формулы закона Ома   следует, что при   ток в контуре максимален и, ввиду чисто активного сопротивления цепи, совпадает по фазе с приложенным напряжением:  Напряжение на индуктивности и на емкости равны и в Q раз превышают приложенное напряжение: Величина Q называется добротностью контура и показывает во сколько раз напряжение на реактивном (индуктивном или емкостном) элементе превышает напряжение на входе схемы в резонансном режиме.  где ρ – волновое (характеристическое) сопротивление контура: Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой: А частота, при которой возникает резонанс – соответственно резонансной частотой.

3 Рис 1. Векторная диаграмма.

Из треугольника напряжений можно получить треугольник сопротивлений для рассматриваемой цепи, разделив стороны этого треугольника на комплексный ток (рис.2 а), из которого следует, что

Z S

X =XL-XC

j j Q

R P

Рис.2. Треугольники сопротивлений и мощностей.

Полученные выражения (2) показывают, что угол сдвига фаз j между током I и напряжением U питающей сети зависят от характера сопротивлений, включенных в цепь переменного тока.

Умножив стороны треугольника сопротивлений на квадрат тока в цепи I2, получим треугольник мощностей (рис.2 б). Активная мощность цепи переменного тока

P=S cosj

Или 

Из треугольников сопротивлений и мощностей можно установить взаимосвязь между параметрами электрической цепи:

 (3)

Применяя закон Ома, можно записать формулы для расчета мощностей:

S=I2Z=U2/Z; P=I2R=U2/R,   (4)

В разветвленной электрической цепи при равенстве индуктивного и емкостного сопротивлений (XL=XC) разность фаз напряжения и тока на входе цепи равна нулю и полное сопротивление цепи

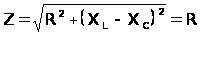 тогда   и   (5,6)

Это состояние называется резонансом напряжения.

Анализ представленных выражений показывает, что резонанс напряжений характеризуется рядом существенных факторов:

1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению.

2. Из этого следует, что при малом значении активного сопротивления ток может достигать большого значения.

3. Коэффициент мощности при резонансе

принимает наибольшее значение, которому соответствует угол j=0. Это означает, что вектор тока I и вектор напряжения U совпадают по направлению.

Активная мощность P=RI2 имеет наибольшее значение, равное полной мощности S, в то же время реактивная мощность цепи Q=I2X=I2 (XL-XC) оказывается равной нулю:

Q=QL-QC=0.

При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности QL=QC=XLI2=XCI2 могут приобретать теоретически, в зависимости от значения тока и реактивных сопротивлений, величину, большую, чем полная мощность S.

5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными UC=UL=XCI=IXL и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжения питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е. UR=U.

Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи.

В то же время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике, электронике и различного рода приборах и устройствах, основанных на резонансе напряжений.

6. Исследование резонансных явлений в электротехнических устройствах удобно проводить с использованием резонансных кривых: изменение тока, коэффициента мощности, напряжения на катушке, напряжения на батарее конденсаторов и полного сопротивления электрической цепи в зависимости от емкости конденсаторов. В радиотехнических устройствах резонансные кривые строятся также в зависимости от индуктивности катушки LК или частоты входного сигнала.

2. Задание по работе

1. Произвести экспериментальное исследование цепи с последовательным соединением катушки индуктивности, конденсатора и активного сопротивления.

По экспериментальным данным произвести расчет параметров соответствующих элементов электрической цепи (R, RK, LK, C, XL, XC).

3. По полученным данным построить векторные диаграммы для трех случаев: ХL>XC; ХL=XC; ХL<XC.

4. Составить краткие выводы по работе.

5. Ответить на вопросы самоконтроля.

3. Методические указания к выполнению работы

1. Записать в отчет по лабораторной работе технические данные приборов и оборудования, используемого при выполнении работы.

Собрать электрическую цепь согласно схеме рис.3.

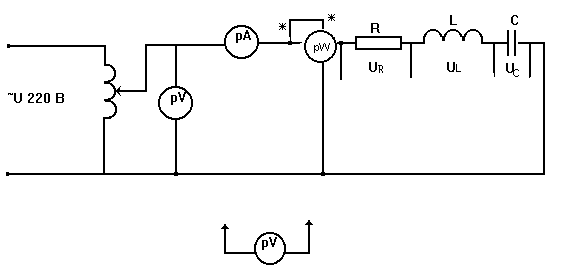
Рис.3. Схема исследования.

3. Для измерения напряжений предусмотреть два вольтметра со свободными концами на 300 и 60 В.

Изменяя емкость конденсаторной батареи произвести измерения необходимых величин (4...5 опытов), результаты измерений записать в таблицу.

Исследование цепи с последовательным соединением R, L, C.

Измерено

Вычислено

C

U

UR

UK

UC

I

P

R

RK

ZK

Z

XC

cosj

мкФ

В

В

В

В

А

Вт

Ом

Ом

Ом

Ом

Ом

-

5. Вычисление полного сопротивления цепи Z и катушки ZL, активного R, индуктивного XL и емкостного XC сопротивлений, индуктивности L и емкости С, падения напряжения на индуктивности UL и коэффициента мощности cosj производить по формулам:

6. Питание электрической цепи осуществлять от регулируемого источника питания синусоидального напряжения, расположенного на панели источника питания (лабораторный автотрансформатор - ЛАТР). Перед включением необходимо убедиться, что ручка регулятора источника питания находится в крайнем левом положении. В режиме исследований максимальное напряжение на входных зажимах должно быть не выше 120 - 130 В (для ограничения тока).

7. Для получения достоверных результатов необходимо выбрать оптимальный предел измерения регистрирующего прибора и не допускать ошибок при определении цены деления прибора.

4 В состав цепей переменного тока входят резистивные элементы, катушки индуктивности, конденсаторы и эле­менты, соединенные магнитной или емкостной связью с другими цепями. В резистивных элементах электрическая энергия пре­образуется в другие виды энергии. Резистивный элемент характеризуется значением сопротивления и обладает не^ которой индуктивностью и емкостью, влиянием которых¹ в ряде случаев можно пренебречь (например, при низкой частоте). Индуктивный элемент кроме индуктивности обладает также сопротивлением, которым, как правило, пренебречь нельзя. Иногда учитывается и влияние емкости. В емкостном элементе имеются некоторые потери энер-гии, но они относительно невелики, и поэтому их можно не учитывать. Процессы в цепях переменного тока отличаются от процессов в цепях постоянного тока, токи и напряже­ния которых неизменны. При неизменных токах в цепи не изменяются электрические и магнитные поля, связанные с цепью. В цепях переменного тока при изменениях на­пряжений и токов изменяются магнитные и электрические •поля, связанные с цепью. При изменениях магнитных полей возникают ЭДС самоиндукции и взаимоиндукции, а при изменениях электрических полей в цепи протекают зарядные и разрядные токи. •В цепях переменного тока, как и постоянного, пока­зываются условные положительные направления ЭДС, напряжений и токов. Синусоидальные переменные величины можно графически изображать при помощи синусоид или вращающих-,ся векторов. Соотношение между отдельными электрическими величинами, выраженное графически в форме си­нусоид, называется синусоидальной диаграммой. В этом 'Случае ординаты синусоиды в определенном масштабе ^представляют собой мгновенные значения величины (ток, 5 напряжение, ЭДС), а абсциссы — промежутки времени от '.начала отсчета. Соотношение между отдельными электрическими величинами (ток, напряжение, ЭДС) одной частоты, выра-женное графически в форме векторов, называется векторной диаграммой. '- Вектор — это отрезок, характеризующий численное значение и направление той или иной измеряемой величины. Длина вектора в масштабе выражает амплитуду• синусоиды. Угол, образованный вектором и положительным направлением оси абсцисс, в начальный момент равен начальной фазе, а частота вращения вектора равна угловой частоте. Векторы одноименных величин изображаются в одном и том же масштабе, и их взаимное расположение не изменяется, так как они вращаются с одинаковой угловой скоростью. Мгновенные значения синусоидальной величины выра­жаются проекциями вращающегося вектора на ось ординат. За положительное направление вращения векторов принято направление, обратное движению часовой 'Стрелки 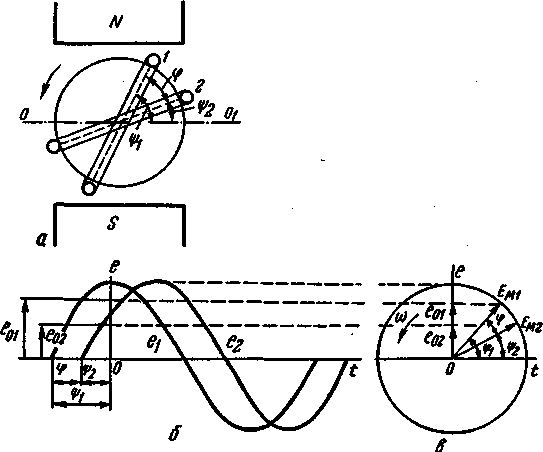 Рис. 19. Положение витков якоря генератора (а); синусоидаль­ная (б) и векторная (в) диа­граммы ЭДС в витках / и 2. На одной векторной диаграмме изображаются лишь те электрические величины, которые имеют одну и ту же частоту. Один из векторов на диаграмме располагают произвольно, все прочие векторы по отношению к нему — под углами, определяемыми разностью (сдвигом) фаз.  Синусоидальная и векторная диаграммы ЭДС в вит­ках / и .2, расположенных на якоре генератора (рис. 19, а) и имеющих соответственно начальные фазы \|)i и $2, показаны на рис. 19,6 и в.