22. Поведение аналитической функции в окрестности устранимой особой точки и существенно особой точки.

23. Поведение аналитической функции в окрестности полюса. Теорема о связи между нулем и полюсом функции.

24. Классификация бесконечно удаленных особых точек аналитической функции.

Окрестностью точки z=∞называется внешность какого-либо круга с центром в точке О и достаточно большим радиусом R. Точка z=∞называется изолированной особой точкой, если в некоторой окресности нет других особых точек функции . Если z=∞устранимая особая точка, то разложение функции в Ряд Лорана в окресности этой точки, не имеет членов с положительными показателями. Если z=∞ полюс, то в разложении конечное число членов с положительным показателем. Если z=∞ существенно особой точкой, то будет бесконечно много членов с положительными показателями z=1/w, w→0,z→∞при f(1/w)при w→0.

25. Понятие вычета и основная теорема Коши о вычетах.

Вычетом функции в изолированной особой точке называется интеграл 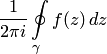, где — контур, принадлежащий окрестности точки и охватывающий ее. Обход контура — положительный, т.е. область им ограниченная и принадлежащая окрестности при обходе расположена слева: для — обход против часовой стрелки (рис. 4.2,а), для — по часовой стрелке. Обозначается вычет

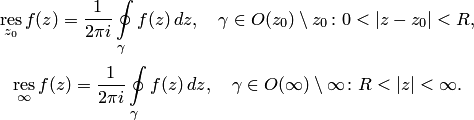
Основная теорема о вычетах

Утверждение 4.6 (основная теорема о вычетах). Если функция -аналитическая в за исключением конечного числа особых точек , то справедливо равенство (где — граница области ):

Обобщенная теорема о вычетах

Утверждение 4.7 (обобщенная теорема о вычетах). Сумма вычетов функции во всех ее особых точках, включая бесконечно удаленную точку, равна нулю:

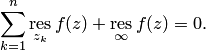
26. Правила вычисления вычетов.

Теоретический минимум

Вычетом функции в особой точке z=a по определению называется величина

Контур интегрирования должен охватывать только одну особую точку z=a, причём она должна быть изолированной

и являться точкой однозначного характера.

Обычно по определению вычеты не вычисляют: это неудобно. Можно показать, что вычет функции в точке представляет собой

коэффициент при минус первой степени в разложении функции в ряд Лорана в окрестности данной точки. Это упрощает вычисление,

так как появляется возможность использовать приёмы разложения функции в ряд Лорана, не связанные с вычислением контурных

интегралов. Тут многое зависит от вида особой точки. В разложении функции в ряд Лорана в окрестности устранимой особой точки

отрицательные степени отсутствуют. Следовательно, и вычет в такой точке равен нулю. Разложение в ряд Лорана в окрестности полюса

содержит конечное число отрицательных степеней. В этом случае для полюса n-го порядка

Чаще всего применяется именно эта формула. Для простого полюса (полюса первого порядка) формула сильно упрощается:

Отдельно рассматривается вычет в бесконечно удалённой точке. Он равен взятому с противоположным знаком коэффициенту при минус первой степени разложения функции в ряд Лорана в окрестности бесконечно удалённой точки.

Вычеты находят применение при вычислении интегралов по основной теореме о вычетах.